Có hai chiếc thang dài như nhau được dựa vào một bức tường với cùng độ cao BH = B’H’ như Hình 4.55. Các góc BAH và B'A'H có bằng nhau không? Vì sao?
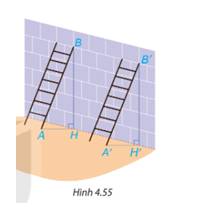
Có hai chiếc thang dài như nhau được dựa vào một bức tường với cùng độ cao BH = B’H’ như Hình 4.55. Các góc BAH và B'A'H có bằng nhau không? Vì sao?

Mỗi hình sau có các cặp tam giác vuông nào bằng nhau? Vì sao?
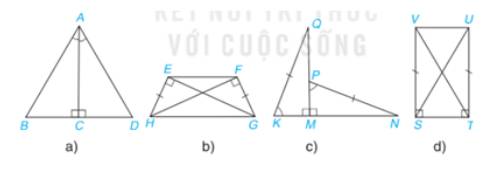
Thảo luận (1)Hướng dẫn giảia) Xét 2 tam giác vuông ABC và ADC có:
\(\widehat {ACB} = \widehat {ACD}( = 90^\circ )\)
AC chung
\(\widehat {BAC} = \widehat {DAC}\)(gt)
=>\(\Delta ABC = \Delta ADC\)(g.c.g)
b) Xét 2 tam giác vuông HEG và GFH có:
HE=GF(gt)
HG chung
=>\(\Delta HEG = \Delta GFH\)(cạnh huyền - cạnh góc vuông)
c) Xét 2 tam giác vuông QMK và NMP có:
QK=NP(gt)
\(\widehat K = \widehat P\)(gt)
=>\(\Delta QMK = \Delta NMP\)(cạnh huyền – góc nhọn)
d) Xét 2 tam giác vuông VST và UTS có:
VS=UT(gt)
ST chung
=>\(\Delta VST = \Delta UTS\)(2 cạnh góc vuông)
(Trả lời bởi Hà Quang Minh)
Cho hình 4.56, biết AB=CD, \(\widehat {BAC} = \widehat {BDC} = {90^o}\). Chứng minh rằng \(\Delta ABE = \Delta DCE\).

Thảo luận (1)Hướng dẫn giảiVì tổng 3 góc trong 1 tam giác luôn bằng 180 độ.
Xét hai tam giác AEB và DEC có:
\(\widehat {AEB} = \widehat {DEC}\)(đối đỉnh) và \(\widehat {BAC} = \widehat {BDC} = {90^o}\).
Suy ra: \(\widehat {ABE} = \widehat {DCE}\)
Xét 2 tam giác AEB và DEC có:
\(\widehat {BAC} = \widehat {BDC} (= {90^o}\))
\(AB=DC\) (gt)
\(\widehat {ABE} = \widehat {DCE}\) (cmt)
=>\(\Delta AEB = \Delta DEC\)(g.c.g)
(Trả lời bởi Hà Quang Minh)
Cho hình chữ nhật ABCD, M là trung điểm của cạnh BC.
Chứng minh rằng \(\Delta ABM = \Delta DCM\).
Thảo luận (1)Hướng dẫn giải
Vì ABCD là hình chữ nhật nên AB=DC; \(\widehat{ABM}=\widehat{DCM}=90^0\) (tính chất hình chữ nhật)
Xét 2 tam giác ABM và DCM có:
AB=DC (cmt)
\(\widehat{ABM}=\widehat{DCM}\) (cmt)
BM=CM (gt)
=>\(\Delta ABM = \Delta DCM\)(c.g.c)
(Trả lời bởi Kiều Sơn Tùng)