Bài 20:
a: Qua O, kẻ tia OE nằm giữa hai tia OA và OC sao cho OE//AB//CD
OE//AB
=>\(\hat{AOE}=\hat{OAB}\) (hai góc so le trong)
=>\(\hat{AOE}=30^0\)
OE//CD
=>\(\hat{EOC}=\hat{OCD}\) (hai góc so le trong)
=>\(\hat{EOC}=45^0\)
Ta có: tia OE nằm giữa hai tia OA và OC
=>\(\hat{AOC}=\hat{AOE}+\hat{COE}=30^0+40^0=75^0\)
b: Gọi F là giao điểm của AO và CD
Ta có: AF//IM
=>\(\hat{AFM}+\hat{IMF}=180^0\) (hai góc trong cùng phía)(1)
Ta có: AI//FM
=>\(\hat{IAF}+\hat{AFM}=180^0\) (hai góc trong cùng phía)(2)
Từ (1),(2) suy ra \(\hat{IAF}=\hat{IMF}\)
=>\(\hat{IMF}=45^0\)
Bài 21:
a: Dx//BC
=>\(\hat{xDC}=\hat{DCB}\) (hai góc so le trong)
=>\(\hat{DCB}=70^0\)
=>\(\hat{ACB}=70^0\)
b: Xét ΔABC có \(\hat{ABC}+\hat{ACB}+\hat{BAC}=180^0\)
=>\(\hat{ABC}=180^0-40^0-70^0=70^0\)
Ta có: \(\hat{DAB}+\hat{BAC}=180^0\) (hai góc kề bù)
=>\(\hat{DAB}=180^0-40^0=140^0\)
Ta có: Ay là phân giác của góc DAB
=>\(\hat{yAD}=\hat{yAB}=\frac12\cdot\hat{DAB}=\frac{140^0}{2}=70^0\)
Ta có: \(\hat{yAD}=\hat{ACB}\left(=70^0\right)\)
mà hai góc này là hai góc ở vị trí đồng vị
nên Ay//BC
c: Xét ΔABC có \(\hat{ABC}=\hat{ACB}\left(=70^0\right)\)
nên ΔABC cân tại A
ΔABC cân tại A
mà AH là đường cao
nên AH là phân giác của góc BAC














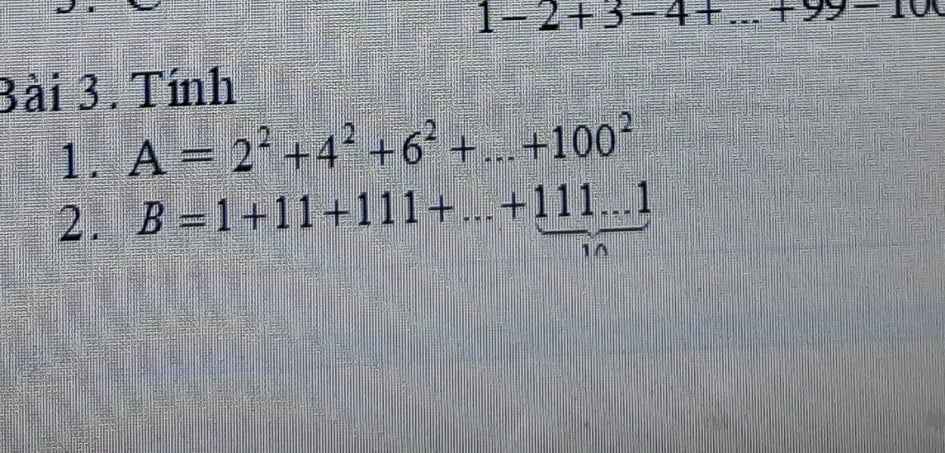 giúp em câu a. E tsu dag cần gấp mng giúp em với. Em cảm ơn
giúp em câu a. E tsu dag cần gấp mng giúp em với. Em cảm ơn
