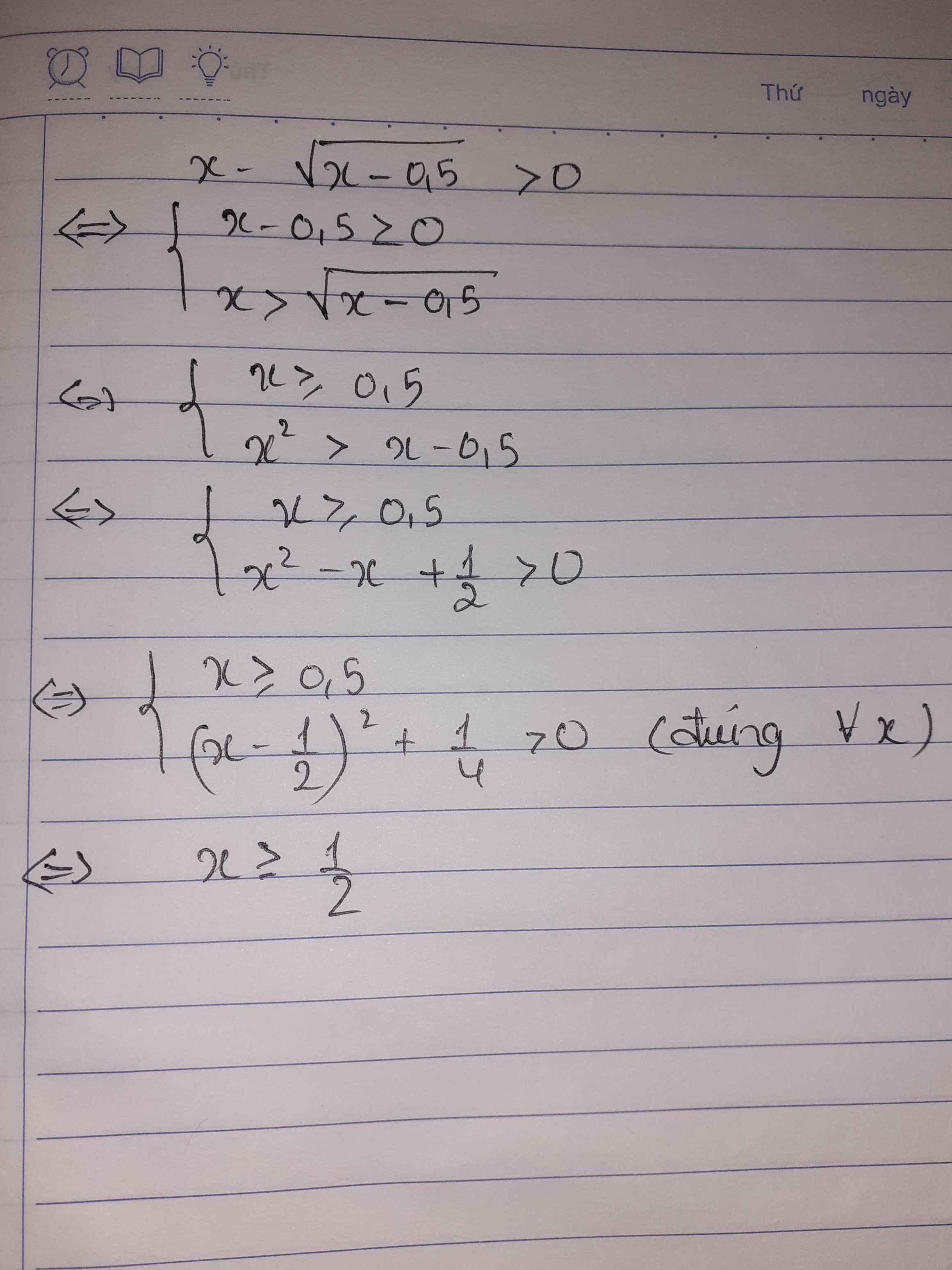Ta có: \(x-\sqrt{x-0.5}>0\)
\(\Leftrightarrow\sqrt{x-\dfrac{1}{2}}< x\)
\(\Leftrightarrow\left\{{}\begin{matrix}0\le x-\dfrac{1}{2}\\x-\dfrac{1}{2}\le x^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ge\dfrac{1}{2}\\x^2-x+\dfrac{1}{2}\ge0\end{matrix}\right.\)
\(\Leftrightarrow x\ge\dfrac{1}{2}\)
\(x>\sqrt{x-\dfrac{1}{2}}\Leftrightarrow x^2>x-\dfrac{1}{2}\Leftrightarrow x^2-x-\dfrac{1}{2}>0\Leftrightarrow\text{x}^2-x+\dfrac{1}{4}-\dfrac{3}{4}>0\Leftrightarrow\left(x-\dfrac{1}{2}\right)^2-\dfrac{3}{4}>0\\ \left\{{}\begin{matrix}x-\dfrac{1}{2}< -\dfrac{\sqrt{3}}{2}\rightarrow x< \dfrac{1-\sqrt{3}}{2}\\x-\dfrac{1}{2}>\dfrac{\sqrt{3}}{2}\rightarrow x>\dfrac{1+\sqrt{3}}{2}\end{matrix}\right.\)
Lời giải:
ĐKXĐ: $x\geq 0,5$
BPT $\Leftrightarrow x> \sqrt{x-0,5}$
$\Leftrightarrow x^2>x-0,5$ (do $x\geq 0,5$)
$\Leftrightarrow x^2-x+0,5>0$
$\Leftrightarrow (x-\frac{1}{2})^2+0,25>0$ (luôn đúng)
Vậy BPT có nghiệm $x\geq 0,5$