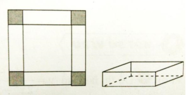
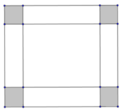
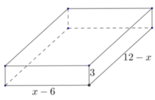
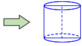
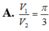Từ một tấm bìa hình chữ nhật có chiều rộng 30cm và chiều dài 80cm (hình a) người ta cắt ở bốn góc bốn hình vuông có cạnh x(cm) với 5 ≤ x ≤ 10 và gấp lại để tạo thành chiếc hộp có dạng hình hộp chữ nhật không nắp (hình b). Tìm x để thể tích chiếc hộp là lớn nhất (kết quả làm tròn đến hàng phần trăm).
Ta có CD : 80 - 2x
CR : 30 - 2x
Chiều cao : x
Ta có \(V=x\left(80-2x\right)\left(30-2x\right)=x\left(2400-220x+4x^2\right)\)
\(=2400x-220x^2+4x^3\)
\(V'=2400-440x+12x^2=0\Leftrightarrow x=30;x=\dfrac{20}{3}\)
Để V max => x = 20/3
Đúng 0
Bình luận (3)
