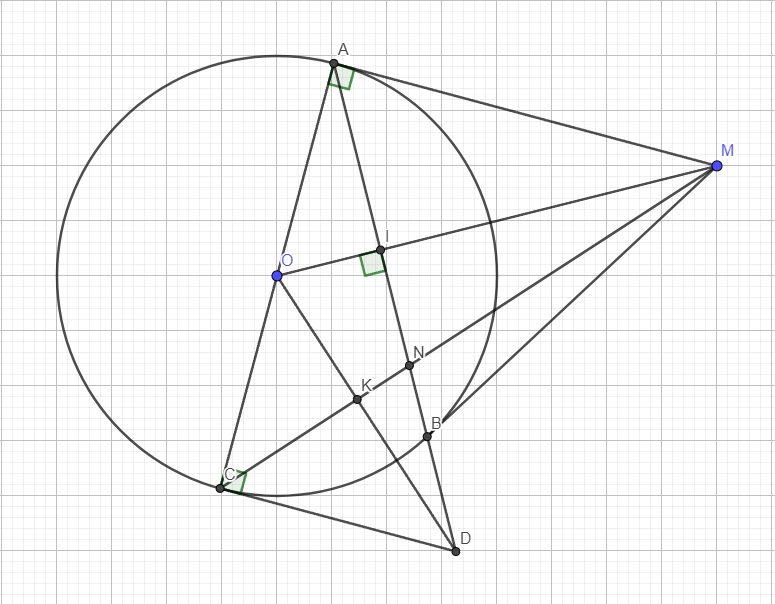
Em coi lại đề, từ điểm M làm sao vẽ các tiếp tuyến AB, AC được nhỉ? Sau đó lại đường kính AC nữa, nghĩa là AC vừa là tiếp tuyến vừa là đường kính?
a. Ý này đơn giản em tự chứng mình
b.
Ta có \(\widehat{IAO}=\widehat{AMO}\) (cùng phụ \(\widehat{AOM}\))
\(\Rightarrow\Delta_VACD\sim\Delta_VMAO\left(g.g\right)\)
\(\Rightarrow\dfrac{AC}{AM}=\dfrac{CD}{OA}=\dfrac{CD}{OC}\) (do OA=OC)
\(\Rightarrow\dfrac{AC}{CD}=\dfrac{AM}{OC}\)
\(\Rightarrow\Delta_VACM\sim\Delta_VCDO\left(c.g.c\right)\)
\(\Rightarrow\widehat{COD}=\widehat{AMC}\)
Mà \(\widehat{AMC}+\widehat{OCK}=90^0\) (tam giác ACM vuông tại A)
\(\Rightarrow\widehat{COD}+\widehat{OCK}=90^0\Rightarrow\widehat{OKC}=90^0\)
\(\Rightarrow\Delta_VMKO\sim\Delta_VMIN\) (chung góc \(\widehat{OMK}\))
\(\Rightarrow\dfrac{MK}{IM}=\dfrac{MO}{MN}\Rightarrow MN.MK=MI.MO\)
Mặt khác theo hệ thức lượng trong tam giác vuông MAO với đường cao AI:
\(MA^2=MI.MO\)
\(\Rightarrow MA^2=MN.MK\)