Đáp án D.
Gọi z = x + y i x , y ∈ ℝ ⇒ M x ; y biểu diễn số phức z
Do z 16 có phần thực là và phần ảo thuộc đoạn 0 ; 1 nên
0 ≤ x 16 ≤ 1 0 ≤ y 16 ≤ 1 ⇒ 0 ≤ x , y ≤ 16
Mặt khác 16 z ¯ = 16 z z 2 = 16 x + y i x 2 + y 2 có phần thực là và phần ảo thuộc đoạn 0 ; 1 nên
x , y ≤ 0 16 x x 2 + y 2 ≤ 1 16 y x 2 + y 2 ≤ 1 ⇔ x 2 + y 2 − 16 x ≥ 0 x 2 + y 2 − 16 y ≥ 0
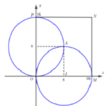
Minh họa hình vẽ, ta có phương trình đường thẳng OA là y = x , phương trình
x 2 + y 2 − 16 x = 0 ⇒ y = 16 x − x 2 y ≥ 0
Diện tích cần tìm là miền nằm ngoài 2 đường tròn x 2 + y 2 − 16 x = 0 và x 2 + y 2 − 16 y = 0 và nằm trong hình vuông MNPQ.
Diện tích hình quạt I O A ⏜ là S q u a t = 1 4 π 8 2 = 16 π ; S Δ I O A = 32
Diện tích phần giới hạn bởi cung OA và dây OA là S = 16 π − 32
Suy ra diện tích miền giao nhau của 2 đường tròn là: S G = 2 S = 32 π − 2 .
Diện tích cần tìm là:
S c t = 16 2 − π 8 2 + 32 π − 2 = 192 − 32 π = 32 6 − π



