Trong hình 40a, ta có góc \(\widehat {{A_1}}\) là một góc nhọn.
Trong hình 40b thì ta có 4 góc tại đỉnh A là một góc vuông.
Trong hình 40a, ta có góc \(\widehat {{A_1}}\) là một góc nhọn.
Trong hình 40b thì ta có 4 góc tại đỉnh A là một góc vuông.
Tính số đo góc giữa hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) trong môi trường hợp sau:
a) \({\Delta _1}:\left\{ \begin{array}{l}x = - 3 + 3\sqrt 3 t\\y = 2 + 3t\end{array} \right.\) và \({\Delta _2}:y - 4 = 0\)
b) \({\Delta _1}:2x - y = 0\) và \({\Delta _2}: - x + 3y - 5 = 0\)
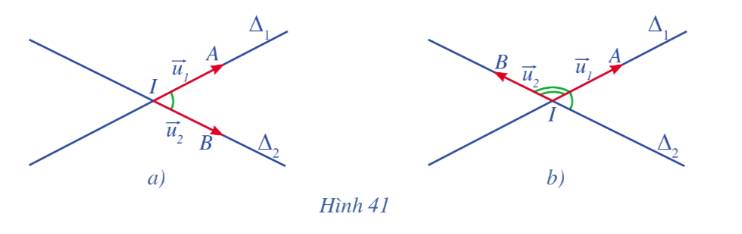
Cho hai đường thẳng \({\Delta _1},{\Delta _2}\)cắt nhau tại I và có vectơ chỉ phương lần lượt là \(\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} \). Gọi A và B là các điểm lần lượt thuộc hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) sao cho \(\overrightarrow {{u_1}} = \overrightarrow {IA} ,\overrightarrow {{u_2}} = \overrightarrow {IB} \).
a) Quan sát Hình 41a, Hình 41b, hãy nhận xét về độ lớn của góc giữa hai đường thẳng
\({\Delta _1},{\Delta _2}\)và độ lớn của góc giữa hai vectơ \(\overrightarrow {IA} \),\(\overrightarrow {IB} \)
b) Chứng tỏ cos(\({\Delta _1},{\Delta _2}\)) = \(\left| {cos\left( {\overrightarrow {IA} ,{\rm{ }}\overrightarrow {IB} } \right)} \right|\).
Với giá trị nào của tham số m thì hai đường thẳng sau đây vuông góc?
\({\Delta _1}:mx - y + 1 = 0\) và \({\Delta _2}:2x - y + 3 = 0\).
Trong mặt phẳng toạ độ, cho hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) có vectơ chỉ phương lần lượt là\(\overrightarrow {{u_1}} = {\rm{ }}\left( {{a_1};{\rm{ }}{b_1}} \right),{\rm{ }}\overrightarrow {{u_2}} {\rm{ }} = {\rm{ }}\left( {{a_2};{b_2}} \right)\) . Tính \(\cos \left( {{\Delta _1},{\Delta _2}} \right)\).
Trong mặt phẳng toạ độ, cho hai đường thẳng \({\Delta _1},{\Delta _2}\) lần lượt có vectơ chỉ phương là \(\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} \). Nêu điều kiện về hai vectơ \(\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} \) trong môi trường hợp sau:
a) \({\Delta _1}\) cắt \({\Delta _2}\)
b) \({\Delta _1}\)song song với \({\Delta _2}\)
c), \({\Delta _1}\) trùng với \({\Delta _2}\)
a) Tính khoảng cách từ điểm \(O\left( {0{\rm{;}}0} \right)\) đến đường thẳng \(\Delta \):\(\frac{x}{{ - 4}} + \frac{y}{2} = 1\)
b) Tính khoảng cách giữa hai đường thẳng song song \({\Delta _1}:x - y + 1 = 0\)và \({\Delta _2}:x - y - 1 = 0\)
Cho ba điểm A(2;- 1), B(1 ; 2) và C(4;- 2). Tính số đo góc BAC và góc giữa hai đường thẳng AB, AC.
Trong mặt phẳng toạ độ, cho đường thẳng \(\Delta \): 2x + y– 4 = 0 và điểm M(-1; 1). Gọi H là hình chiếu của M lên đường thẳng \(\Delta \).
a) Tìm một vectơ chỉ phương của đường thẳng MH.
b) Viết phương trình tham số của đường thẳng MH.
c) Tìm toạ độ của H. Từ đó, tính độ dài đoạn thẳng MH.
Xét vị trí tương đối của hai đường thẳng \({\Delta _1}:\left\{ \begin{array}{l}x = 1 + {t_1}\\y = - 2 + {t_1}\end{array} \right.\) và \({\Delta _2}:\left\{ \begin{array}{l}x = 2{t_2}\\y = - 3 + 2{t_2}\end{array} \right.\)