Các câu hỏi tương tự
Xét các hình trụ có tổng độ dài đường sinh và bán kính đường tròn đáy bằng 2 thì hình trụ có thể tích lớn nhất
V
m
a
x
bằng bao nhiêu?
Đọc tiếp
Xét các hình trụ có tổng độ dài đường sinh và bán kính đường tròn đáy bằng 2 thì hình trụ có thể tích lớn nhất V m a x bằng bao nhiêu?
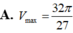
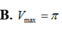
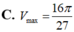
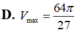
Trong tất cả các hình trụ mà tổng độ dài đường sinh và bán kính đường tròn đáy bằng 1 thì hình trụ có thể tích lớn nhất
V
m
a
x
bằng bao nhiêu?
Đọc tiếp
Trong tất cả các hình trụ mà tổng độ dài đường sinh và bán kính đường tròn đáy bằng 1 thì hình trụ có thể tích lớn nhất V m a x bằng bao nhiêu?
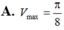
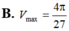
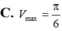
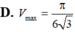
Xét các trụ tròn có tổng bình phương của đường sinh và bán kính đường tròn bằng 3, hình trụ có thể tích lớn nhất
V
m
a
x
bằng bao nhiêu?
Đọc tiếp
Xét các trụ tròn có tổng bình phương của đường sinh và bán kính đường tròn bằng 3, hình trụ có thể tích lớn nhất V m a x bằng bao nhiêu?
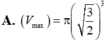
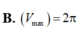
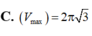
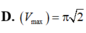
Cho hình trụ tròn xoay có độ dài đường sinh bằng đường kính đáy và thể tích khối trụ bằng
16
π
. Diện tích toàn phần của khối trụ đã cho bằng
Đọc tiếp
Cho hình trụ tròn xoay có độ dài đường sinh bằng đường kính đáy và thể tích khối trụ bằng 16 π . Diện tích toàn phần của khối trụ đã cho bằng
![]()
![]()
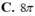
![]()
Một khối trụ có khoảng cách giữa hai đáy, độ dài đường sinh và bán kính đường tròn đáy lần lượt bằng h, l, r. Khi đó công thức tính diện tích toàn phần của khối trụ là
Đọc tiếp
Một khối trụ có khoảng cách giữa hai đáy, độ dài đường sinh và bán kính đường tròn đáy lần lượt bằng h, l, r. Khi đó công thức tính diện tích toàn phần của khối trụ là
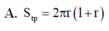
![]()
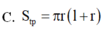
![]()
Cho khối trụ có bán kính đáy R và có chiều cao h2R. Hai đáy của khối trụ là hai đường tròn có tâm lần lượt là O và O. Trên đường tròn (O) ta lấy điểm A cố định. Trên đường tròn (O) ta lấy điểm B thay đổi. Hỏi độ dài đoạn AB lớn nhất bằng bao nhiêu?
Đọc tiếp
Cho khối trụ có bán kính đáy R và có chiều cao h=2R. Hai đáy của khối trụ là hai đường tròn có tâm lần lượt là O và O'. Trên đường tròn (O) ta lấy điểm A cố định. Trên đường tròn (O') ta lấy điểm B thay đổi. Hỏi độ dài đoạn AB lớn nhất bằng bao nhiêu?
![]()
![]()
![]()
![]()
Cho khối trụ có bán kính đáy R và có chiều cao h 2R . Hai đáy của khối trụ là hai đường tròn có tâm lần lượt là O và O’. Trên đường tròn (O) ta lấy điểm A cố định. Trên đường tròn (O’) ta lấy điểm B thay đổi. Hỏi độ dài đoạn AB lớn nhất bằng bao nhiêu?
Đọc tiếp
Cho khối trụ có bán kính đáy R và có chiều cao h = 2R . Hai đáy của khối trụ là hai đường tròn có tâm lần lượt là O và O’. Trên đường tròn (O) ta lấy điểm A cố định. Trên đường tròn (O’) ta lấy điểm B thay đổi. Hỏi độ dài đoạn AB lớn nhất bằng bao nhiêu?
![]()
![]()
![]()
![]()
Một khối trụ có trục là một đường kính của mặt cầu (S) bán kính R, các đường tròn đáy đều thuộc mặt cầu, biết hình trụ đó có bán kính đường tròn đáy và đường sinh bằng nhau. Tính tỉ số thể tích
V
1
của hình trụ đó với
V
2
là thể tích mặt cầu.
Đọc tiếp
Một khối trụ có trục là một đường kính của mặt cầu (S) bán kính R, các đường tròn đáy đều thuộc mặt cầu, biết hình trụ đó có bán kính đường tròn đáy và đường sinh bằng nhau. Tính tỉ số thể tích V 1 của hình trụ đó với V 2 là thể tích mặt cầu.
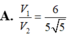
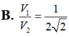
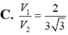
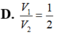
Một khối đồ chơi gồm một khối trụ và một khối nón có cùng bán kính được chồng lên nhau, độ dài đường sinh khối trụ bằng độ dài đường sinh khối nón và bằng đường kính của khối trụ, khối nón (tham khảo hình vẽ). Biết thể tích của toàn bộ khối đồ chơi là 50
c
m
3
, thể tích khối trụ gần với số nào nhất trong các số sau
Đọc tiếp
Một khối đồ chơi gồm một khối trụ và một khối nón có cùng bán kính được chồng lên nhau, độ dài đường sinh khối trụ bằng độ dài đường sinh khối nón và bằng đường kính của khối trụ, khối nón (tham khảo hình vẽ). Biết thể tích của toàn bộ khối đồ chơi là 50 c m 3 , thể tích khối trụ gần với số nào nhất trong các số sau
![]()
![]()
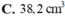
![]()



