Question

Trong các hình chữ nhật có chu vi là 24cm, hãy tìm hình chữ nhật có diện tích lớn nhất.

Answer 1

Gọi chiều dài của hình chữ nhật là x (cm, \(0 < x < 12\))

Chiều rộng của hình chữ nhật là \(12 - x\left( {cm} \right)\)

Diện tích của hình chữ nhật là: \(x\left( {12 - x} \right) =  - {x^2} + 12x\;\left( {c{m^2}} \right)\)

Đặt \(S\left( x \right) =  - {x^2} + 12x,x \in \left( {0;12} \right)\)

\(S'\left( x \right) =  - 2x + 12,S'\left( x \right) = 0 \Leftrightarrow x = 6\left( {tm} \right)\)

Bảng biến thiên: 

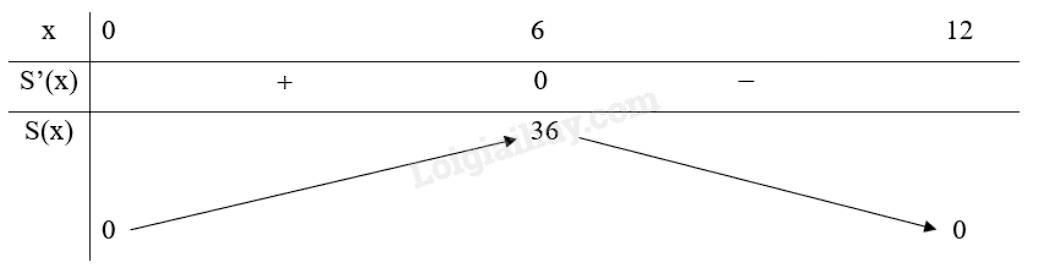
Do đó, trong các hình có cùng chu vi thì hình chữ nhật có diện tích lớn nhất là \(36c{m^2}\).