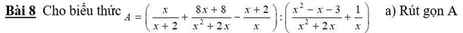Diện tích xung quanh là:
\(\dfrac{1}{2}\cdot5\cdot C_{đáy}=\dfrac{5}{2}\cdot6\cdot4=24\cdot\dfrac{5}{2}=60\left(cm^2\right)\)
Gọi O là tâm của đáy ABCD
=>SO là trung đoạn của hình chóp S.ABCD
Kẻ SH\(\perp\)BC
=>SH là đường cao của hình chóp S.ABCD
Theo đề, ta có: SO=5cm; AB=BC=CD=DA=6cm
ΔSBC cân tại S
mà SH là đường cao
nên H là trung điểm của BC
Xét ΔCAB có
O,H lần lượt là trung điểm của CA,CB
=>OH là đường trung bình của ΔCAB
=>\(OH=\dfrac{1}{2}AB=3\left(cm\right)\)
ΔSHO vuông tại H
=>\(SH^2+HO^2=SO^2\)
=>\(SH=\sqrt{5^2-3^2}=4\left(cm\right)\)
\(S_{tp}=S_{xq}+S_{đáy}\)
\(=60+6^2=96\left(cm^2\right)\)
\(V_{S.ABCD}=\dfrac{1}{3}\cdot SH\cdot S_{ABCD}=\dfrac{1}{3}\cdot4\cdot6^2=48\left(cm^3\right)\)