Ta có: OA = OC (bán kính) nên ΔOAC cân tại O.
Lại có O'A = O'D (bán kính) nên ΔO'AD cân tại O'
Vậy OC // O'D (có hai góc so le trong bằng nhau).
Trên hình 89, hai đường tròn tiếp xúc nhau tại A. Chứng minh rằng OC // O'D.
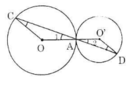
Hình 89
Cho hai đường tròn (O) và (O’) tiếp xúc ngoài với nhau tại A. Qua A kẻ một cát tuyến bất kỳ cắt (O) tại C và (O’) tại D. Chứng minh rằng OC // O’D
Cho hình bên, trong đó hai đường tròn (O) và (O’) tiếp xúc với nhau tại A. Chứng minh rằng các tiếp tuyến Bx và Cy song song với nhau.
Cho đường tròn (O) và đường thẳng xy tiếp xúc với đường tròn tại A. Vẽ đường tròn (I) đường kính OA.
a) Chứng minh rằng hai đường tròn (O) và (I) tiếp xúc với nhau
b) Vẽ dây cung AC của (O) cắt I tại một điểm thứ hai là M. Chứng minh MA=MC
c) đường thẳng OM cắt xy tại B. Chứng minh rằng BC là tiếp tuyến của (O)
Cho đường tròn tâm (O) và dây cung AB. M là điểm trên AB. Dựng đường tròn (O1) qua A , M và tiếp xúc với (O), đường tròn (O2) qua M , B và tiếp xúc với (O), hai đường tròn này cắt nhau tại điểm thứ hai là N. Chứng minh rằng MNO^=90o.
Cho hai đường tròn (O) và (O’) tiếp xúc với nhau tại A như hình bên. Chứng minh rằng các bán kính OB và O’C song song với nhau.
Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Dây AC của đường tròn (O) tiếp xúc với đường tròn (O’) tại A. Dây AD của đường trong (O’) tiếp xúc với đường tròn (O) tại A. Gọi K là điểm đối xứng với A qua trung điểm I của OO’, E là điểm đối xứng với A qua B. Chứng minh rằng: Bốn điểm A, C, E, D cùng nằm trên một đường tròn
Cho nửa đường tròn (O) đường kính AB. Vẽ bán kính OC ⊥ AB. Lấy điểm M trên nửa đường tròn. Tiếp tuyến tại M cắt OC và cắt tiếp tuyến tại A ở hai điểm D, E. AE cắt BD tại F. Chứng minh rằng EA · EF không đổi khi M di động trên đường tròn.
Cho hai đường tròn (O) và (O’) tiếp xúc ngoài với nhau tại B. Vẽ đường kính AB của đường tròn (O) và đường kính BC của đường tròn (O’). Đường tròn đường kính OC cắt (O) tại M và N. a/ Đường thẳng CM cắt (O’) tại P. Chứng minh: OM//BP. b/ Từ C kẻ đường thẳng vuông góc với CM cắt tia ON tại D. Chứng minh: Tam giác OCD là tam giác cân.
