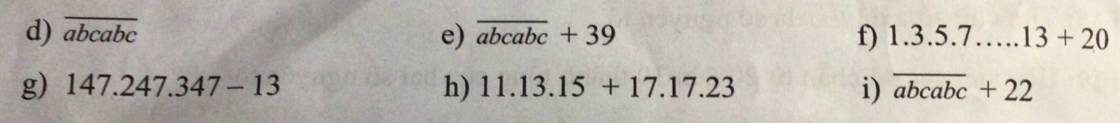Question

Tổng (hiệu) sau là số nguyên tố hay hợp số:

CÁC BẠN GIẢI CHI TIẾT RA GIÚP MÌNH NHÉ! CẢM ƠN CÁC BẠN RẤT NHIỀU! 🤧✨💖

Answer 1

Lời giải:

d. 

$\overline{abcabc}=\overline{abc}\times 1000+\overline{abc}=\overline{abc}\times 1001$ là hợp số 

e.

$\overline{abcabc}+39=\overline{abc}\times 1001+39$

$=\overline{abc}\times 7\times 11\times 13+13\times 3$

$=13\times (\overline{abc}\times 77+3)$ là hợp số

f. 

$1.3.5.7...13+20=5\times (1.3.7...13+4)$ là hợp số 

g.

$147.247.347-13=147.13.19.347-13=13(147.19.347-1)$ là hợp số

h.

$11.13.15+17.17.23$ chẵn và lớn hơn $2$ nên là hợp số

i.

$\overline{abcabc}+22=\overline{abc}\times 1001+22=\overline{abc}\times 11\times 91+2\times 11$

$=11\times (\overline{abc}\times 91+2)$ là hợp số.