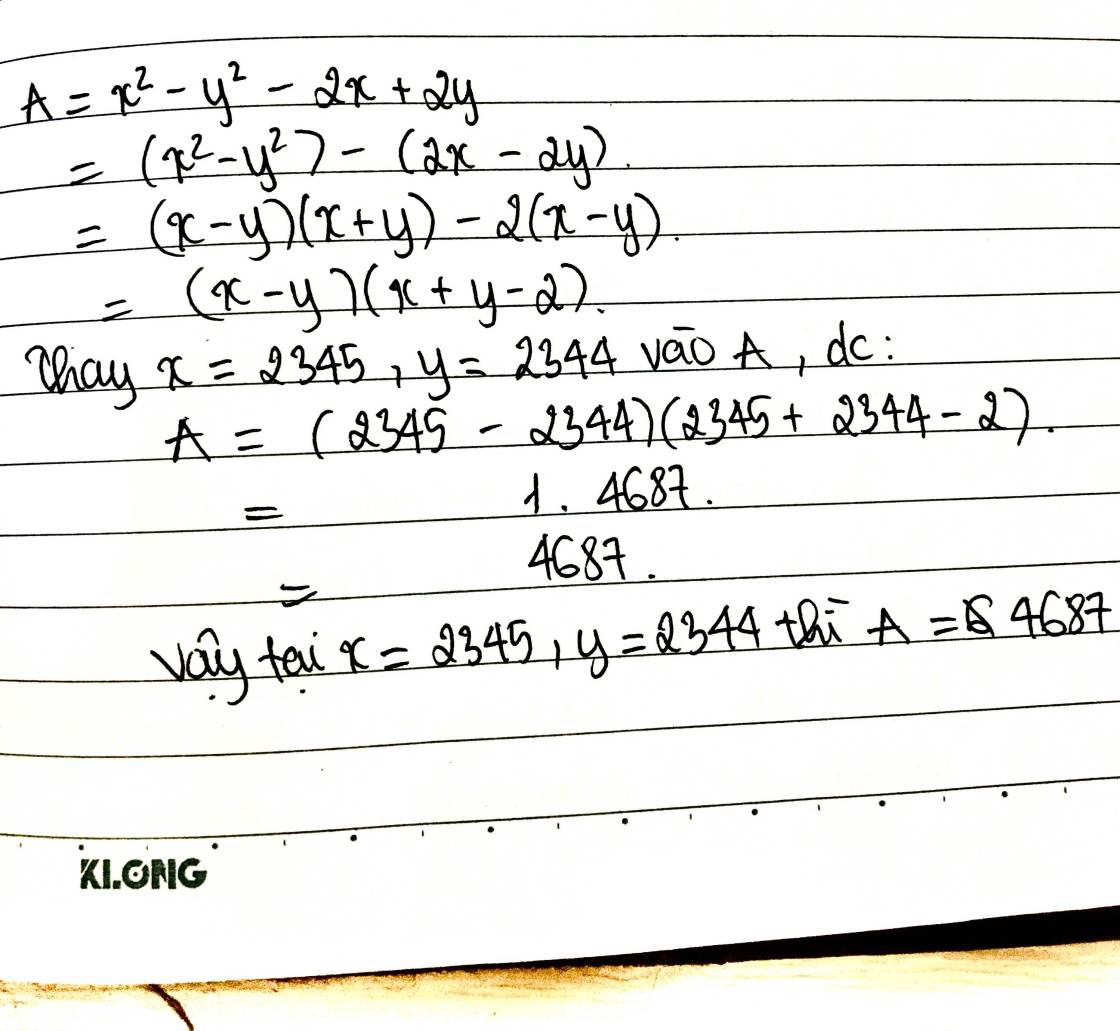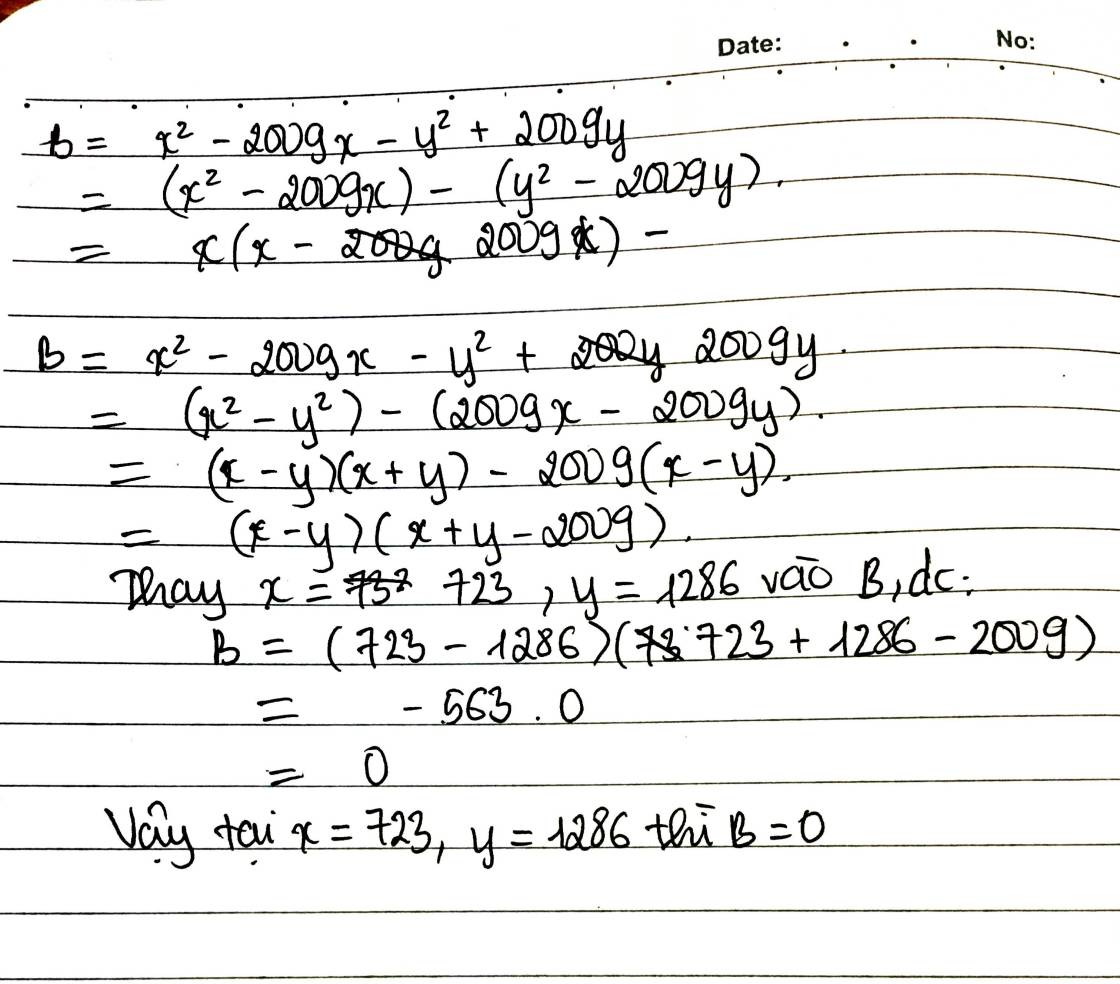\(A=x^2-y^2-2x+2y\\=(x^2-y^2)-(2x-2y)\\=(x-y)(x+y)-2(x-y)\\=(x-y)(x+y-2)\)
Thay \(x=2345;y=2344\) vào A, ta được:
\(A=(2345-2344)(2345+2344-2)\\=1.(4689-2)=4687\)
Vậy $A=4687$ tại $x=2345;y=2344$.
$------$
\(B=x^2-2009x-y^2+2009y\\=(x^2-y^2)-(2009x-2009y)\\=(x-y)(x+y)-2009(x-y)\\=(x-y)(x+y-2009)\)
Thay \(x=723;y=1286\) vào B, ta được:
\(B=(723-1286)(723+1286-2009)\\=-563.(2009-2009)=0\)
Vậy $B=0$ tại $x=723;y=1286$.
$\text{#}Toru$