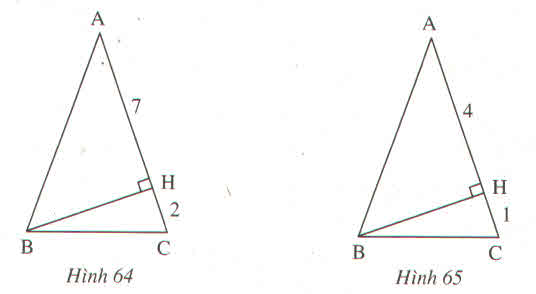
câu a: có 2 bước
bước 1 : tính cạnh BH
ta có: AB = AC = 7 +2 =9
theo định lý Py -ta -go:
ta có : BH2 = AB2- HB2
BH2= 92-72
=>BH=\(\sqrt{32}\)
bước 2: tính cạnh BC
theo định lí Py-ta-go
ta có: BH2 + HC2=BC2
=>BC2= \(\sqrt{32}\)2 + 22 =36
=> BC = \(\sqrt{36}\) = 6
câu b: có 2 bước
bước 1: tìm cạnh BH
ta có AB = AC= 4+1=5
theo định lí Py-ta-go
ta có BH2 = AB2 - AH2
BH2 = 52-42
=> BH= 3
bước 2 : tìm cạnh BC
theo định lí Py-ta-go
ta có : BC2= HC2+BH2
BC2= 12+32
=>BC=\(\sqrt{10}\)
a)Xét tam giác ABC cân tại A\(\Rightarrow\)AB = AC 1
Mà AC = AH + HC =7 + 2 = 9 (cm) 2
Từ 1 và 2 \(\Rightarrow\)AB = AC = 9 (cm)
Xét tam giác ABH vuông tại H
Áp dụng định lí Py-ta-go,ta có:
AB2 = BH2 + AH2
\(\Rightarrow\)92 = BH2 + 72
BH2 = 92 - 72
BH2 = 81 - 49
BH2 = 32\(\Rightarrow\)BH = \(\sqrt[]{32}\) (cm)
Xét tam giác BHC vuông tại H
Áp dụng định lí Py-ta-go, ta có:
BC2 = BH2 + HC2
\(\Rightarrow\)BC2 = \(\sqrt[]{32}\)2 + 22
BC2 = 32 + 4
BC2 = 36\(\Rightarrow\)BC = 6 (cm)
b)Xét tam giác ABC cân tại A\(\Rightarrow\)AB = AC 1
Mà AC = AH + HC = 4 + 1 = 5 (cm) 2
Từ 1 và 2 \(\Rightarrow\)AB = AC = 5 (cm)
Xét tam giác ABH vuông tại H
Áp dụng định lí Py-ta-go, ta có:
AB2 = HB2 + AH2
\(\Rightarrow\)52 = HB2 + 42
HB2 = 52 - 42
HB2 = 25 - 16
HB2 = 9 \(\Rightarrow\)HB = 3 (cm)
Xét tam giác BHC vuông tại H
Áp dụng định lí Py-ta-go, ta có:
BC2 = HC2 + BH2
\(\Rightarrow\)BC2 = 12 + 32
BC2 = 1 + 9
BC2 = 10\(\Rightarrow\)BC = \(\sqrt[]{10}\) (cm)