(x2 - 4 ) . (6-2x) = 0
=> x2 - 4 hoặc 6 - 2x = 0 hoặc cả hai bằng 0
Nếu cả hai số bằng 0 => vô lí vì x2 -4 và 6-2x không thể bằng nhau
Xét 2 trường hợp còn lại
TH1 : x2 - 4 = 0
=> x2 = 4
=> x2 = 22
=> x =2
Vậy x=2
TH2 : 6-2x = 0
=> 2x = 6 - 0
=> 2x =6
=> x = 6:2
=> x =3
Vậy x = 3
Kết luận chung x=2 hoặc x=3
(x2 - 4)(6 - 2x) = 0
=> (x - 2)(x + 2)(6 - 2x) = 0
=> \(\hept{\begin{cases}x-2=0\\x+2=0\\6-2x=0\end{cases}}\)
=> \(\hept{\begin{cases}x=2\\x=-2\\2x=6\end{cases}}\)
=> \(\hept{\begin{cases}x=2\\x=-2\\x=3\end{cases}}\)
Vậy ....
Lời giải:
Tập xác định của phương trình
Biến đổi vế trái của phương trình
Phương trình thu được sau khi biến đổi
Lời giải thu được










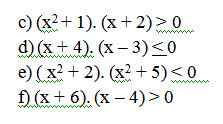 Giúp mình với, mình cần gấp ạ
Giúp mình với, mình cần gấp ạ






