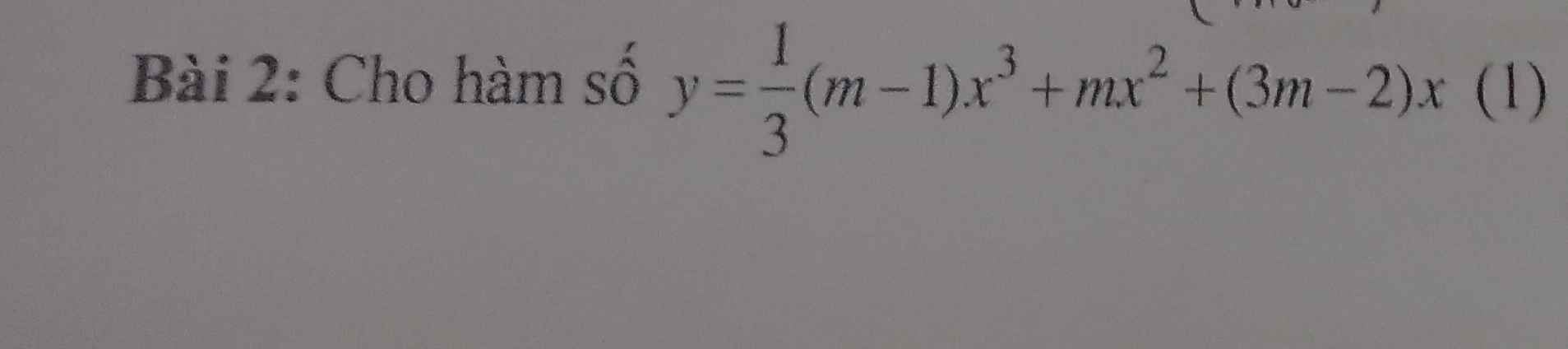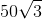TXĐ: \(D=R\)
Hàm số \(y=\dfrac{1}{3}\left(m-1\right)x^3+mx^2+\left(3m-2\right)x\) đồng biến trên TXĐ:
\(\Leftrightarrow\left\{{}\begin{matrix}a>0\\\Delta'y'=b^2-3ac\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{3}\left(m-1\right)>0\\m^2-3\cdot\dfrac{1}{3}\left(m-1\right)\cdot\left(3m-2\right)\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>1\\-2m^2+5m-2\le0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m>1\\\left[{}\begin{matrix}m\le\dfrac{1}{2}\\m\ge2\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}m\le\dfrac{1}{2}\\m\ge2\end{matrix}\right.\) thỏa mãn ycbt.