Violympic toán 9
Các câu hỏi tương tự
a) tìm số tự nhiên x và số nguyên y thỏa mãn: \(x^2y+2xy+x^2-2018x+y=-1\)
b) giải hệ phương trình \(\left\{{}\begin{matrix}x^2-2y^2+xy=2y-2x\\\sqrt{x+2y+1}+\sqrt{x^2+y+2}=4\end{matrix}\right.\)
Tìm nghiệm nguyên không âm thỏa mãn phương trình: x^2=y^2 + căn y+1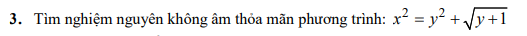
Tìm các cặp số nguyên (x;y) thỏa mãn : \(x^2y+xy-2x^2-3x+4=0\)
Cho HPT: \(\left\{{}\begin{matrix}x-2y=4m-5\\2x+y=3m\end{matrix}\right.\). Tìm m để hệ phương trình có nghiệm (x;y) thỏa mãn: \(\dfrac{2}{x}-\dfrac{1}{y}=-1\)
Cho HPT: \(\left\{{}\begin{matrix}x-2y=4m-5\\2x+y=3m\end{matrix}\right.\). Tìm m để hệ phương trình có nghiệm (x;y) thỏa mãn: \(\dfrac{2}{x}-\dfrac{1}{y}=-1\)
(6-15GP/1 câu) Chứng mịnh định lí Fermat đơn giản, theo hiểu biết của kiến thức Toán học phổ thông:1. Chứng minh rằng có vô số nghiệm nguyên dương (x,y,z) thỏa mãn x^2+y^2z^2.2. Chứng minh rằng có vô số nghiệm nguyên dương (x,y,z) thỏa mãn x^2+y^2z^3.3. Chứng minh rằng không có nghiệm nguyên dương (x,y,z) thỏa mãn x^3+y^3z^3.4. Nếu ta thay z^3 thành z^5, bài toán số 2 có còn đúng không? Vì sao?
Đọc tiếp
(6-15GP/1 câu) Chứng mịnh định lí Fermat đơn giản, theo hiểu biết của kiến thức Toán học phổ thông:
1. Chứng minh rằng có vô số nghiệm nguyên dương (x,y,z) thỏa mãn \(x^2+y^2=z^2\).
2. Chứng minh rằng có vô số nghiệm nguyên dương (x,y,z) thỏa mãn \(x^2+y^2=z^3\).
3. Chứng minh rằng không có nghiệm nguyên dương (x,y,z) thỏa mãn \(x^3+y^3=z^3\).
4. Nếu ta thay \(z^3\) thành \(z^5\), bài toán số 2 có còn đúng không? Vì sao?
Tìm các số nguyên dương x và y thỏa mãn: \(\dfrac{2x+2y}{xy+2}\) có giá trị là 1 số nguyên
Cho x,y,z >0 thỏa mãn \(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}=3\). Tìm GTLN của biểu thức \(P=\dfrac{1}{\sqrt{5x^2+2xy+2y^2}}+\dfrac{1}{\sqrt{5y^2+2yz+2z^2}}+\dfrac{1}{\sqrt{5z^2+2xz+2x^2}}\)
a) Tìm cặp số x,y nguyên dương thỏa mãn \(x^2+y^2\left(x-y+1\right)-\left(x-1\right)y=22\)
b) Tìm các cặp số x,y,z nguyên dương thỏa mãn \(\dfrac{xy+yz+zx}{x+y+z}=4\)







