Các câu hỏi tương tự
Kí hiệu S(t) là diện tích của hình phẳng giới hạn bởi các đường y=2x+1, y=0, x=1, x=t (t>1). Tìm t để S(t)=10
A. t=4
C. t=13
C. t=3
D. t=4
Trong không gian với hệ tọa độ Oxyz, cho bốn đường thẳng
D
1
:
x
−
2
1
y
+
2
−
1
z
−
1
−
1
;
...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho bốn đường thẳng
D 1 : x − 2 1 = y + 2 − 1 = z − 1 − 1 ; D 2 : x − 1 1 = y − 1 2 = z − 1 ; D 3 : x − 1 = y + 2 1 = z + 1 1
và đường thẳng D 4 : x − 5 1 = y − a 3 = z − b 1 . Biết không tồn tại đường thẳng nào trong không gian mà cắt được đồng thời cả bốn đường thẳng trên. Tính giá trị của biểu thức T = a - 2b.
A. T = -2
B. T = -3
C. T = 2
D. T = 3
Tìm cosin góc giữa 2 đướng thẳng
∆
1
:
2
x
+
y
+
1
0
và
∆
2
:
x
2
+
t
y
1
-...
Đọc tiếp
Tìm cosin góc giữa 2 đướng thẳng ∆ 1 : 2 x + y + 1 = 0 và ∆ 2 : x = 2 + t y = 1 - t
A. 10 10
B. 3/10
C. 3/5
D. 3 10 10
Trong không gian với hệ tọa độ Oxyz cho đường thẳng
d
:
{
x
1
-
t
y
2
+
2
t
z...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho đường thẳng d : { x = 1 - t y = 2 + 2 t z = 3 + t và mặt phẳng P : x - y + 3 = 0 . Tính số đo góc giữa đường thẳng d và mặt phẳng (P).
A. 60 °
B. 30 °
C. 120 °
D. 45 °
Cho hình thang cong (H) giới hạn bởi các đường
y
3
x
, y0, x0, x2. Đường thẳng x1 (0t2) chia (H) thành hai phần có diện tích
S
1
và
S
2
(như hình vẽ). Tìm t để
S
1
3
S
2
A.
t
log
3
5...
Đọc tiếp
Cho hình thang cong (H) giới hạn bởi các đường y = 3 x , y=0, x=0, x=2. Đường thẳng x=1 (0<t<2) chia (H) thành hai phần có diện tích S 1 và S 2 (như hình vẽ). Tìm t để S 1 = 3 S 2
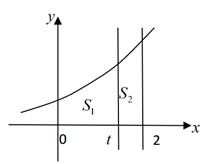
A. t = log 3 5
B. t = log 3 2
C. t = log 3 35
D. t = log 3 7
Cho x, y là các số thực dương thỏa mãn
5
x
+
2
y
+
3
3
x
y
+
x
+
1
5
x
y
5
+
3
−
x...
Đọc tiếp
Cho x, y là các số thực dương thỏa mãn 5 x + 2 y + 3 3 x y + x + 1 = 5 x y 5 + 3 − x − 2 y + x − 2 . Tìm giá trị nhỏ nhất của biểu thức T = x + y .
A. T min = 2 + 3 2 .
B. T min = 1 + 5 .
C. T min = 3 + 2 3 .
D. T min = 5 + 3 2 .
Cho x,y,z,t EN .Cm rằng x/(x+y+z)+y/(x+y+t)+z/(y+z+t)+t/(z+t+x) có giá trị không phải số tự nhiên
Cho hai số thực x, y thỏa mãn
0
≤
x
≤
1
2
,
0
y
≤
1
và
log
11
−
2
x
−
y
2
y...
Đọc tiếp
Cho hai số thực x, y thỏa mãn 0 ≤ x ≤ 1 2 , 0 < y ≤ 1 và log 11 − 2 x − y = 2 y + 4 x − 1. Xét biểu thức P = 16 x 2 y − 2 x 3 y + 2 − y + 5. Gọi m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của P. Khi đó giá trị của biểu thức T = 4m + M bằng bao nhiêu?
A. 16
B. 18
C. 17
D. 19
Cho hai điểm A(-1;2), B(3;1) và đường thẳng
∆
:
x
1
+
t
y
2
+
t
Điểm C(x;y) thuộc
∆
để tam giác ACB cân tại C. Giá trị x...
Đọc tiếp
Cho hai điểm A(-1;2), B(3;1) và đường thẳng ∆ : x = 1 + t y = 2 + t Điểm C(x;y) thuộc ∆ để tam giác ACB cân tại C. Giá trị x + y là
A. 1
B. 2
C. 5/3
D. 10/3