Chương I - Căn bậc hai. Căn bậc ba
Các câu hỏi tương tự
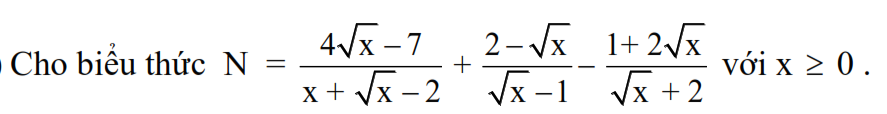
a) Tìm x để N=\(\dfrac{1}{2}\)
b) Tìm x ∈ \(Z\) sao cho N ∈ \(Z\)
c) Tìm GTLN của N
Cho x,y,z dương thỏa \(\dfrac{1}{1+x}+\dfrac{1}{1+y}+\dfrac{1}{1+z}>=2\)
Tìm GTLN của P=xyz
Cho các số thực x, y, z thỏa mãn \(7\left(\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{z^2}\right)=6\left(\dfrac{1}{xy}+\dfrac{1}{yz}+\dfrac{1}{zx}\right)=2016\).
Tìm max: \(P=\dfrac{1}{\sqrt{3\left(2x^2+y^2\right)}}+\dfrac{1}{\sqrt{3\left(2y^2+z^2\right)}}+\dfrac{1}{\sqrt{3\left(2z^2+x^2\right)}}\)
Cho \(B=\dfrac{1}{\sqrt{x}+2}-\dfrac{5}{x-\sqrt{x}-6}+\dfrac{\sqrt{x}-2}{3-\sqrt{x}}\)
a.Rút gọn.
b.Tìm x∈Z để B nguyên.
c.Tìm x để B đạt GTLN.Tính GTLN của B.
Chứng minh bất đẳng thức
Cho x, y, z là các số dương (chứng minh hộ mình phần b) thôi)
a) CMR : 3left(x^2+y^2+z^2right)geleft(x+y+zright)^2
b) Cho x, y, z thỏa mãn : 3+dfrac{1}{x}+dfrac{1}{y}+dfrac{1}{z}12left(dfrac{1}{x^2}+dfrac{1}{y^2}+dfrac{1}{z^2}right)
CMR : dfrac{1}{4x+y+z}+dfrac{1}{x+4y+z}+dfrac{1}{x+y+4z}ledfrac{1}{6}
Đọc tiếp
Chứng minh bất đẳng thức
Cho x, y, z là các số dương (chứng minh hộ mình phần b) thôi)
a) CMR : \(3\left(x^2+y^2+z^2\right)\ge\left(x+y+z\right)^2\)
b) Cho x, y, z thỏa mãn : \(3+\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}=12\left(\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{z^2}\right)\)
CMR : \(\dfrac{1}{4x+y+z}+\dfrac{1}{x+4y+z}+\dfrac{1}{x+y+4z}\le\dfrac{1}{6}\)
Cho x,y,z là các số thực dương thỏa mãn: xyz=1
Tìm giá trị lớn nhất của: \(A=\dfrac{1}{x^3+y^3+1}+\dfrac{1}{y^3+z^3+1}+\dfrac{1}{x^3+z^3+1}\)
Cho x , y , z \(\ne0\) thỏa mãn x + y + z = 0 .
CMR : \(\sqrt{\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{z^2}}=\left|\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right|\)
1) Cho x, y, z ϵ R thỏa mãn:
\(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}=\dfrac{1}{x+y+z}\)
2) Tính giá trị biểu thức:
M = \(\dfrac{3}{4}+\left(x^8-y^8\right)\left(y^9+z^9\right)\left(z^{10}-x^{10}\right)\)
Bài 1. Tìm x, y, z biết: \(\sqrt{x-a}+\sqrt{y-b}+\sqrt{z-c}=\dfrac{1}{2}\left(x+y+z\right)\) (trong đó, a + b + c = 3)
Bài 2.
a) Chứng minh rằng: \(2\left(\sqrt{n+1}-\sqrt{n}\right)< \dfrac{1}{\sqrt{n}}< 2\left(\sqrt{n}-\sqrt{n-1}\right)\)
b/ Cho S = \(1+\dfrac{1}{\sqrt{2}}+\dfrac{1}{\sqrt{3}}+...+\dfrac{1}{\sqrt{100}}\). Chứng minh rằng: 18<S<19











