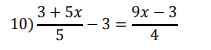Question

Tìm B max biết: B = x² - x

Các bạn trình bày thật rõ ràng ra giúp mình nhé!

Answer 1

\(B=x^2-x\)

\(B=x^2-2\cdot x\cdot\frac{1}{2}+\left(\frac{1}{2}\right)^2-\left(\frac{1}{2}\right)^2\)

\(B=\left(x-\frac{1}{2}\right)^2-\frac{1}{4}\)

mà \(\left(x-\frac{1}{2}\right)^2\ge0\forall x\)

\(\Rightarrow B\ge\frac{1}{4}\forall x\)

Dấu "=" xảy ra \(\Leftrightarrow x-\frac{1}{2}=0\Leftrightarrow x=\frac{1}{2}\)

Vậy Bmin = 1/4 <=> x = 1/2

P.s : đây là tìm B min

Answer 2

Còn cách nữa tìm Bmax :v

Vì \(x^2\ge0\forall x\)

\(\Rightarrow B\le x\forall x\)

Dấu "=" xảy ra \(\Leftrightarrow x^2=0\Leftrightarrow x=0\)

Vậy Bmax = 0 <=> x = 0

Answer 3

Ta có B= x² - x= \(\left(x^2-2.\frac{1}{2}x+\frac{1}{4}\right)-\frac{1}{4}\) =\(\left(x-\frac{1}{2}\right)^2-\frac{1}{4}\) \(\le\frac{-1}{4}\)( vì \(\left(x-\frac{1}{2}\right)^2\ge0\forall x\inℝ\))

Suy ra B\(\le\frac{-1}{4}\)

Dấu "=" xảy ra <=> \(\left(x-\frac{1}{2}\right)^2=0\) <=>\(x-\frac{1}{2}=0\) <=> \(x=\frac{1}{2}\)

Vậy B max =\(\frac{-1}{4}\Leftrightarrow x=\frac{1}{2}\)