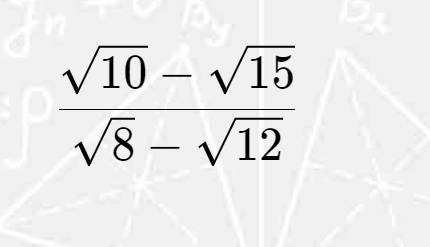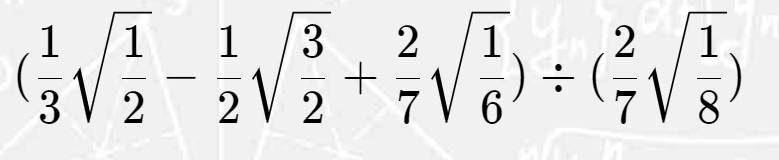Ta có \(\cot\alpha=\tan\beta\) ; \(\cos^2\alpha+\sin^2\alpha=1\)
Khi đó \(-\frac{\cot58^{\text{o}}+\tan27^{\text{o}}}{\cot63^{\text{o}}+\tan32^{\text{o}}}+1=\frac{-\cot58^{\text{o}}-\tan27^{\text{o}}+\cot63^{\text{o}}+\tan32^{\text{o}}}{\cot63^{\text{o}}+\tan32^{\text{o}}}\)
\(=\frac{\left(\tan32^{\text{o}}-\cot58^{\text{o}}\right)+\left(\cot63^{\text{o}}-\tan27^{\text{o}}\right)}{\cot63^{\text{o}}+\tan32^{\text{o}}}=0\)
=> \(\frac{\cot58^{\text{o}}+\tan27^{\text{o}}}{\cot63^{\text{o}}+\tan32^{\text{o}}}=1\)
=> \(\cos^255^{\text{o}}-\frac{\cot58^{\text{o}}+\tan27^{\text{o}}}{\cot63^{\text{o}}+\tan32^{\text{o}}}=\cos^255^{\text{o}}-1=-\sin^255\)