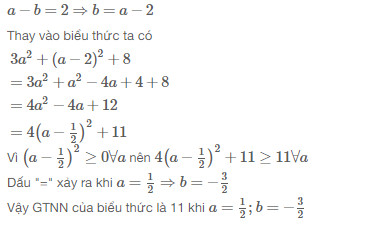Bài 5
\(a - b = 2 <=> b = a - 2\)
Do đó: \(P = 3a^2 + (a-2)^2 + 8\)
\(= 3a^2 + a^2 - 4a + 4 + 8\)
\(= 4a^2 - 4a + 12\)
\(= (2a - 1)^2 + 11\)
Vì \((2a - 1)^2 \geq 0 \) với mọi a nên \(= (2a - 1)^2 + 11 \geq 11 \) hay \(P \geq 11\)
Dấu "=" xảy ra \(\begin{cases} a - b = 2 \\ 2a - 1 = 0 \\\end{cases} <=> \begin{cases} a = \dfrac{1}{2} \\ b = -\dfrac{3}{2} \\\end{cases}\)
Vậy giá trị nhỏ nhất của P là 11 tại \(\begin{cases} a = \dfrac{1}{2} \\ b = -\dfrac{3}{2} \\\end{cases}\)
câu hình:
a) Vì AB là đường kính \(\Rightarrow\angle ADB=90\Rightarrow\angle EDB+\angle EHB=180\)
\(\Rightarrow EDHB\) nội tiếp
b) Xét \(\Delta AHE\) và \(\Delta ADB:\) Ta có: \(\left\{{}\begin{matrix}\angle DABchung\\\angle AHE=\angle ADB=90\end{matrix}\right.\)
\(\Rightarrow\Delta AHE\sim\Delta ADB\left(g-g\right)\Rightarrow\dfrac{AH}{AD}=\dfrac{AE}{AB}\Rightarrow AB.AH=AD.AE\)
mà \(AH.AB=AC^2\) (hệ thức lượng) \(\Rightarrow AC^2=AD.AE\)
c) Vì \(EF\parallel AB\) \(\Rightarrow\angle CFE=\angle CBA=\angle CDA=\angle CDE\)
\(\Rightarrow CDFE\) nội tiếp mà \(\angle CEF=90\) \((EF\parallel AB,AB\bot CH)\)
\(\Rightarrow\angle CDF=90\Rightarrow CD\bot DF\)
Vì \(\Delta CDF\) vuông tại D có K là trung điểm CF \(\Rightarrow KC=KD\)
\(\Rightarrow\Delta KCD\) cân tại K \(\Rightarrow\angle DKB=2\angle DCB=2\angle DAB=\angle DOB\)
\(\Rightarrow DKOB\) nội tiếp \(\Rightarrow K\in\left(OBD\right)\)
Bài 3 :
\(\)Gọi số học sinh hai lớp \(9/1\) và \(9/2\) lần lượt là : \(a,b\)
( ĐK : \(a,b \in \mathbb{N*}\) ; \(a,b< 82\), đơn vị : học sinh )
Tổng học sinh hai lớp là \(82\) nên ta có : \(a+b=82\) (1)
Lại có mỗi học sinh lớp \(9/1\) ủng hộ 4 quyển sách, mỗi học sinh lớp \(9/2\) ủng hộ 3 quyển sách. Tổng số sách là 286 quyển nên ta có : \(4a+3b=286\) (2)
Từ (1) và (2) ta có hệ : \(\left\{{}\begin{matrix}a+b=82\\4a+3b=286\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a=40\\b=42\end{matrix}\right.\) ( thỏa mãn )
Vậy số học sinh lớp \(9/1\) và \(9/2\) lần lượt là \(40\) học sinh và \(42\) học sinh.
Em lỡ bấm gửi nên em gửi tiếp bài 3 ạ:
Giả sử 82 học sinh đều ủng hộ 4 quyển sách thì số sách ủng hộ được là:
82 x 4 = 328(quyển)
số sách chênh lệch vì mỗi bán ủng hộ 3 quyển đã trở thành 4 quyển (chênh 1 quyển)
=> số bạn ủng hộ 3 quyển (số học sinh lớp 9/2) là:
328 - 286 = 42(học sinh)
=> số hs lớp 9/1 là:
82 - 42 = 40(học sinh)