Question

Tam giác ABC có các đường cao BD và CE bằng nhau . Chứng minh rằng tam giác đó là tam giác cân.

Answer 1

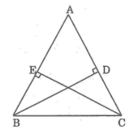
Xét ΔAECvà ΔADB:

GócA:chung (gt)

BD=CE(gt)

Góc D =  Góc E = 90o(gt)

⇒ΔAEC=ΔADB(g.c.g)

mà ΔABCcó AB=AC(ΔAEC=ΔADB0

⇒ΔABCcân tại A.

Answer 2

Xét \(\Delta AEC\)và \(\Delta ADB\):

Góc\(A\):chung (gt)

\(BD=CE\left(gt\right)\)

Góc D =  Góc E = \(90^o\)(gt)

\(\Rightarrow\Delta AEC=\Delta ADB\left(g.c.g\right)\)

mà \(\Delta ABC\)có \(AB=AC\)(\(\Delta AEC=\Delta ADB\)0

\(\Rightarrow\Delta ABC\)cân tại A.

Answer 3

Xét tam giác BEC và tam giác CDB có góc E=góc D=90 độ

cạnh huyền BC chung,

cạnh góc vuông BD=CE

Do đó tam giác BEC=tam giác CDB (cạnh huyền - cạnh góc vuông )

Suy ra góc EBC=góc DCB

Tam giác ABC có hai góc bằng nhau nên là tam giác cân .