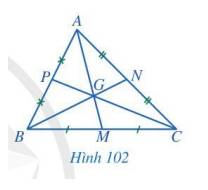
Ba đường trung tuyến AM, BN, CP của tam giác ABC có cùng đi qua một điểm là điểm G.
Bài 10. Tính chất ba đường trung tuyến của tam giác
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
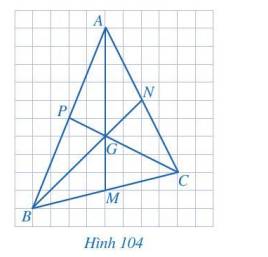
Quan sát các đường trung tuyến AM, BN, CP của tam giác ABC trong Hình 104. Bằng cách đếm số ô vuông, tìm các tỉ số
\(\dfrac{{AG}}{{AM}},\dfrac{{BG}}{{BN}},\dfrac{{CG}}{{CP}}\).
Cho tam giác ABC. Ba đường trung tuyến AM, BN, CP đồng quy tại G. Chứng minh:
\(GA + GB + GC = \dfrac{2}{3}(AM + BN + CP)\).
Cho tam giác ABC có hai đường trung tuyến AM và BN cắt nhau tại G. Gọi H là hình chiếu của A lên đường thẳng BC. Giả sử H là trung điểm của đoạn thẳng BM. Chứng minh:
a) \(\Delta AHB = \Delta AHM\); b) \(AG = \dfrac{2}{3}AB\).
Cho tam giác ABC có hai đường trung tuyến AM và BN cắt nhau tại G. Trên tia đối của tia MA lấy điểm D sao cho MD = MG. Chứng minh:
a) GA = GD;
b) \(\Delta MBG = \Delta MCD\);
c) \(CD = 2GN\).
Hình 107 là mặt cắt đứng của một ngôi nhà ba tầng có mái dốc. Mỗi tầng cao 3,3 m. Mặt cắt mái nhà có dạng tam giác ABC cân tại A với đường trung tuyến AH dài 1,2 m. Tại vị trí O là trọng tâm tam giác ABC, người ta làm tâm cho một cửa sổ có dạng hình tròn.a) AH có vuông góc với BC không? Vì sao?b) Vị trí O ở độ cao bao nhiêu mét so với mặt đất.
Đọc tiếp
Hình 107 là mặt cắt đứng của một ngôi nhà ba tầng có mái dốc. Mỗi tầng cao 3,3 m. Mặt cắt mái nhà có dạng tam giác ABC cân tại A với đường trung tuyến AH dài 1,2 m. Tại vị trí O là trọng tâm tam giác ABC, người ta làm tâm cho một cửa sổ có dạng hình tròn.
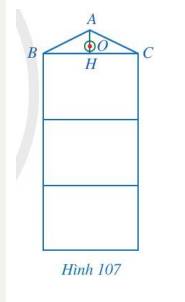
a) AH có vuông góc với BC không? Vì sao?
b) Vị trí O ở độ cao bao nhiêu mét so với mặt đất.
Cho tam giác PQR có hai đường trung tuyến QM và RK cắt nhau tại G. Gọi I là trung điểm của cạnh QR. Chứng minh rằng ba điểm P, G, I thẳng hàng.
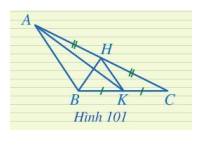
Trong Hình 101, đoạn thẳng HK là đường trung tuyến của những tam giác nào?
Cho tam giác ABC cân tại A, hai đường trung tuyến BM và CN cắt nhau tại G. Chứng minh:
a) BM = CN; b) \(\Delta GBC\) cân tại G.
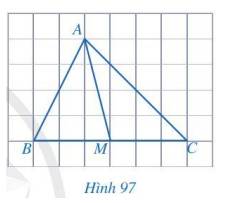
Quan sát Hình 97 và cho biết các đầu mút của đoạn thẳng AM có đặc điểm gì.