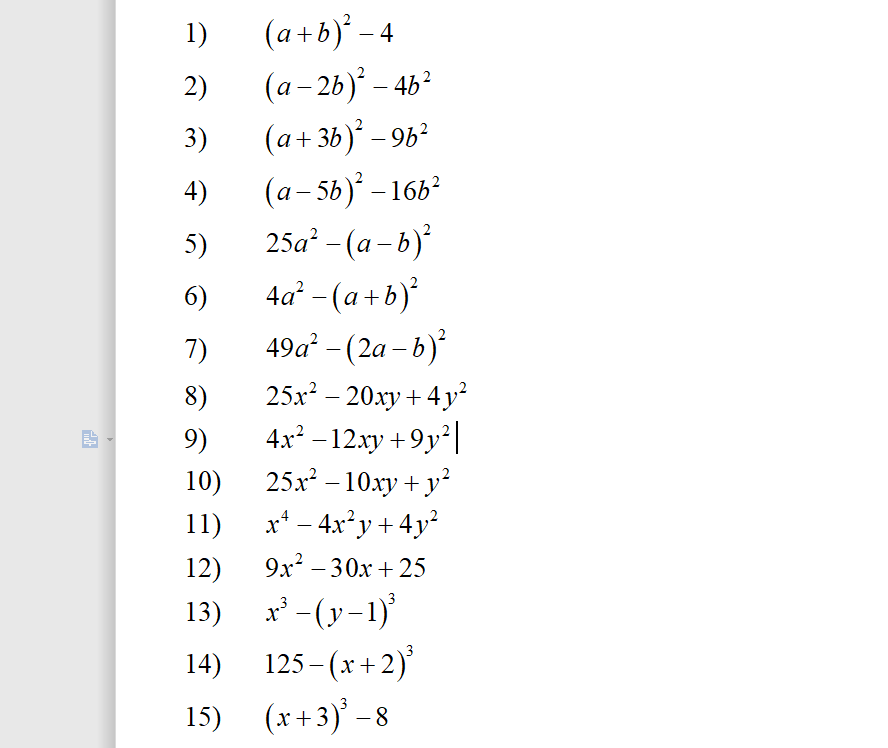
j: \(81x^4+4y^4\)
\(=81x^4+36x^2y^2+4y^4-36x^2y^2\)
\(=\left(9x^2+2y^2\right)^2-\left(6xy\right)^2\)
\(=\left(9x^2+2y^2+6xy\right)\left(9x^2+2y^2-6xy\right)\)
g: \(\left(x^3+x+1\right)\left(x^3+x\right)-2\)
\(=\left(x^3+x\right)^2+\left(x^3+x\right)-2\)
\(=\left(x^3+x+2\right)\left(x^3+x-1\right)\)
\(=\left(x^3+x-1\right)\left(x^3-x+2x+2\right)\)
\(=\left(x^3+x-1\right)\left[x\left(x-1\right)\left(x+1\right)+2\left(x+1\right)\right]\)
\(=\left(x+1\right)\left(x^3+x-1\right)\left(x^2-x+2\right)\)
h: \(\left(x+1\right)\left(x+2\right)\left(x+3\right)\left(x+4\right)+1\)
\(=\left(x^2+5x+4\right)\left(x^2+5x+6\right)+1\)
\(=\left(x^2+5x\right)^2+10\left(x^2+5x\right)+24+1\)
\(=\left(x^2+5x\right)^2+10\left(x^2+5x\right)+25=\left(x^2+5x+5\right)^2\)
j: \(-\left(x^2+2\right)^2+4x\left(x^2+2\right)-3x^2\)
\(=-\left[\left(x^2+2\right)^2-4x\left(x^2+2\right)+3x^2\right]\)
\(=-\left(x^2+2-3x\right)\left(x^2+2-x\right)=-\left(x^2-x+2\right)\left(x-1\right)\left(x-2\right)\)
g) \(\left(x^3+x+1\right)\left(x^3+x\right)-2\)
\(=\left[\left(x^3+x\right)+1\right]\left(x^3+x\right)-2\)
\(=\left(x^3+x\right)^2+\left(x^3+x\right)-2\)
\(=\left(x^3+x\right)^2-\left(x^3+x\right)+2\left(x^3+x\right)-2\)
\(=\left(x^3+x\right)\left(x^3+x-1\right)+2\left(x^3+x-1\right)\)
\(=\left(x^3+x-1\right)\left(x^3+x+2\right)\)
\(=\left(x+1\right)\left(x^2-x+2\right)\left(x^3+x-1\right)\)
h) \(\left(x+1\right)\left(x+2\right)\left(x+3\right)\left(x+4\right)+1\)
\(=\left[\left(x+1\right)\left(x+4\right)\right]\left[\left(x+2\right)\left(x+3\right)\right]+1\)
\(=\left(x^2+5x+4\right)\left(x^2+5x+6\right)+1\)
\(=\left[\left(x^2+5x+5\right)-1\right]\left[\left(x^2+5x+5\right)+1\right]+1\)
\(=\left(x^2+5x+5\right)^2-1+1\)
\(=\left(x^2+5x+5\right)^2\)
i) \(-\left(x^2+2\right)^2+4x\left(x^2+2\right)-3x^2\)
\(=-\left(x^2+2\right)^2+3x\left(x^2+2\right)+x\left(x^2+2\right)-3x^2\)
\(=-\left(x^2+2\right)\left(x^2-3x+2\right)+x\left(x^2-3x+2\right)\)
\(=\left(x^2-3x+2\right)\left(-x^2+x-2\right)\)
\(=\left(x-1\right)\left(x-2\right)\left(-x^2+x-2\right)\)
j) \(81x^4+4y^4\)
\(=\left(9x^2\right)^2+\left(2y^2\right)^2\)
\(=\left(9x^2\right)^2+2\cdot9x^2\cdot2y^2+\left(2y^2\right)^2-2\cdot9x^2\cdot2y^2\)
\(=\left(9x^2+2y^2\right)-36x^2y^2\)
\(=\left(9x^2-6xy+2y^2\right)\left(9x^2+6xy+2y^2\right)\)

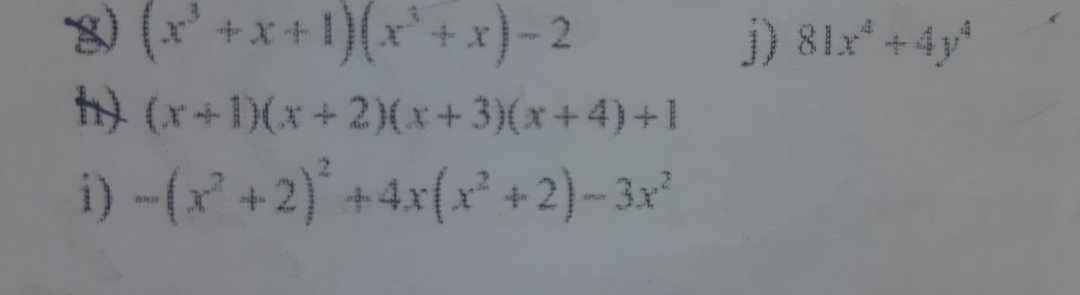












 phân tích đa thức sau thành nhân tử(tách 1 hạng tử thành nhiều hangj tử(kè công thức dùm )
phân tích đa thức sau thành nhân tử(tách 1 hạng tử thành nhiều hangj tử(kè công thức dùm ) phân tích đa thức sau thành nhân tử(tách 1 hạng tử thành nhiều hạng tử)
phân tích đa thức sau thành nhân tử(tách 1 hạng tử thành nhiều hạng tử)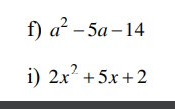 phân tích đa thức sau thành nhân tử(tách 1 hạng tử
phân tích đa thức sau thành nhân tử(tách 1 hạng tử