giải giúp mình với ạa
PHẦN II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1: Cho biểu thức \( P = \frac{\sin^2 x + 3 \sin x \cos x - 4 \cos^2 x}{\tan x - 1} \). Xét tính đúng sai của các khẳng định sau:
a) \(\frac{1}{\cos^2 x} = \tan^2 x + 1\).
b) Biểu thức \( A = \sin^2 x + 3 \sin x \cos x - 4 \cos^2 x \) được viết lại \( A = \frac{\tan^2 x + 3 \tan x - 4}{1 + \tan^2 x} \).
c) Rút gọn biểu thức \( P \) ta được \( P = \frac{\tan x + 4}{1 + \tan^2 x} \).
d) Giá trị của biểu thức \( P \) bằng \(\frac{\sqrt{3}}{4}\) khi \(\cos x = \frac{1}{2}\).
Câu 2: Cho \( A = \frac{\tan^2 x - \sin^2 x + (\sin x + \cos x)^2 - 1}{\tan^2 x \sin^2 x} \) và biểu thức \( B = 1 + 2 \cot^3 x \). Xét tính đúng sai của các khẳng định sau:
a) Biểu thức \((\sin x + \cos x)^2\) bằng \(1 - 2 \sin x \cos x\).
b) \(\tan^2 x - \sin^2 x\) được viết lại \(\tan^2 x \sin^2 x\).
c) Biểu thức \( A \) được đưa về dạng \( A = \frac{\tan^2 x \sin^2 x + 2 \sin x \cos x}{\tan^2 x \sin^2 x} \).
d) Biểu thức \( A \) bằng \( B \).
--------------------HẾT--------------------
Câu 1:
a: Đúng
b: \(A=\sin^2x+3\cdot\sin x\cdot cosx-4\cdot cos^2x\)
\(=1-cos^2x-4\cdot cos^2x+3\cdot\sin x\cdot cosx\)
\(=1-5\cdot cos^2x+3\cdot\sin x\cdot cosx\)
=>\(\frac{1-5\cdot cos^2x+3\cdot\sin x\cdot cosx}{cos^2x}=\frac{1}{cos^2x}-5+3\cdot\frac{\sin x}{cosx}\)
\(=\tan^2x+1-5+3\cdot\tan x=\tan^2x+3\cdot\tan x-4\)
=>\(A\cdot\left(\tan^2x+1\right)=\tan^2x+3\cdot\tan x-4\)
=>\(A=\frac{\tan^2x+3\cdot\tan x-4}{\tan^2x+1}\)
=>Đúng
c: \(P=\frac{\sin^2x+3\cdot\sin x\cdot cosx-4\cdot cos^2x}{\tan x-1}\)
\(=\frac{\tan^2x+3\cdot\tan x-4}{\tan^2x+1}:\left(\tan x-1\right)=\frac{\left(\tan x+4\right)\left(\tan x-1\right)}{\left(\tan x-1\right)\left(\tan^2x+1\right)}=\frac{\tan x+4}{\tan^2x+1}\)
=>Đúng
d: \(\frac{1}{cos^2x}=\tan^2x+1\)
=>\(\tan^2x+1=\frac{1}{\left(\frac12\right)^2}=1:\frac14=4\)
=>\(\tan^2x=3\)
=>\(tanx=\sqrt3\) hoặc \(tanx=-\sqrt3\)
\(P=\frac{\tan x+4}{1+\tan^2x}=\frac{\tan x+4}{4}\)
Khi tan x=\(\sqrt3\) thì \(P=\frac{4+\sqrt3}{4}\)
Khi tan x=-\(\sqrt3\) thì \(P=\frac{4-\sqrt3}{4}\)
=>Sai
Câu 2:
a: \(\left(\sin x+cosx\right)^2=\sin^2x+cos^2x+2\cdot\sin x\cdot cosx\)
\(=1+2\cdot\sin x\cdot cosx\)
=>Đúng
b: \(\tan^2x-\sin^2x\)
\(=\frac{\sin^2x}{cos^2x}-\sin^2x=\sin^2x\left(\frac{1}{cos^2x}-1\right)\)
\(=\sin^2x\cdot\frac{1-cos^2x}{cos^2x}=\sin^2x\cdot\frac{\sin^2x}{cos^2x}=\sin^2x\cdot\tan^2x\)
=>Đúng
c: Sai
d: \(A=\frac{\tan^2x-\sin^2x+\left(\sin x+cosx\right)^2-1}{\tan^2x\cdot\sin^2x}\)
\(=\frac{\tan^2x\cdot\sin^2x-2\cdot\sin x\cdot cosx}{\tan^2x\cdot\sin^2x}=1-\frac{2}{\sin x}\cdot\frac{cosx}{\tan^2x}=1-\frac{2}{\sin x}\cdot\frac{cosx\cdot cos^2x}{\sin^2x}\)
\(=1-\frac{2\cdot cos^3x}{\sin^3x}=1-2\cdot\cot^3x\)
=>Sai





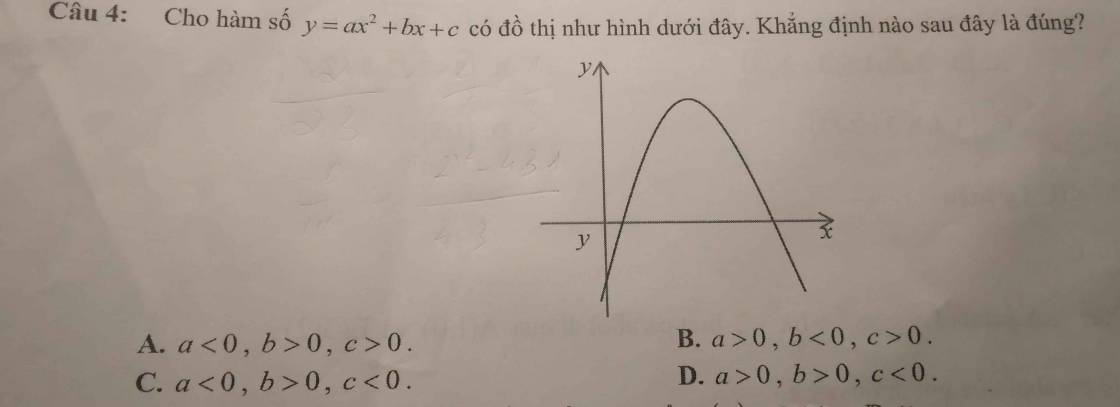



 giúp mình với giải thích cho mình luôn nhé huhu mình cảm ơn
giúp mình với giải thích cho mình luôn nhé huhu mình cảm ơn