Nhờ mọi người giải 2 bài này giúp e với, e cảm ơn nhiều ạ
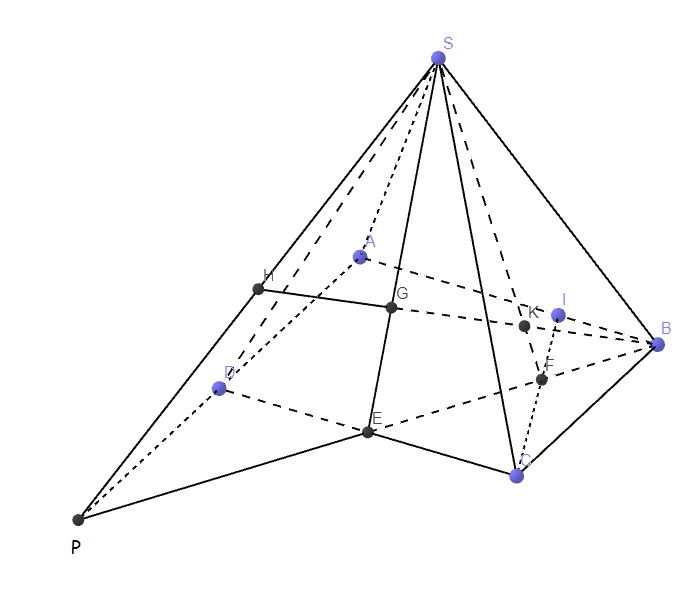
Câu 1. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. G là trọng tâm tam giác SCD, I là điểm thuộc cạnh AB thỏa Al = 21B. Đường thẳng BG cắt mặt phẳng (SIC) và mặt phẳng (SAD) lần lượt tại K, H. Tính tỉ số BK/BH (kết quả làm tròn đến hàng phần trăm).
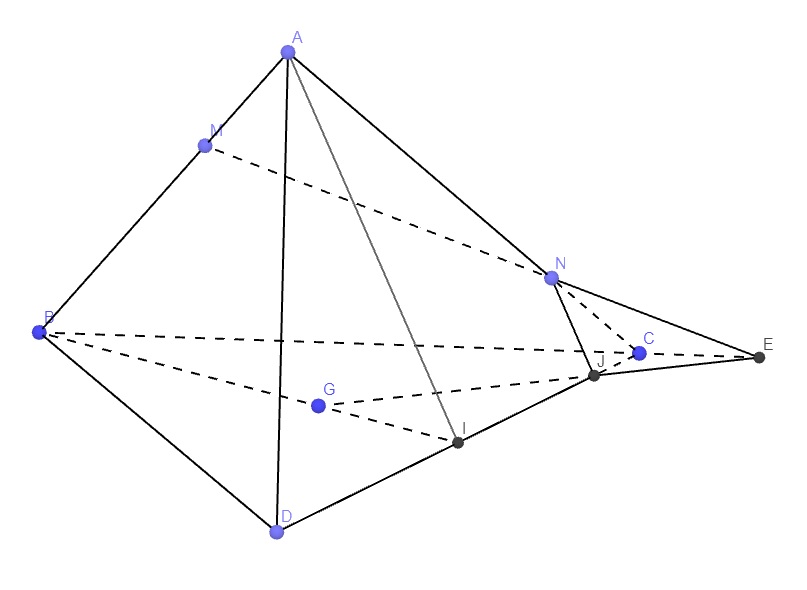
Câu 2. Cho tứ diện ABCD, M là điểm thuộc AB sao cho AM/AB=1/3 và N là điểm thuộc AC mà AN = 3NC; Gọi I là trung điểm của CD. G là trọng tâm tam giác BCD. Gọi J là giao điểm của CD và mặt phẳng (MNG). Vị trí tương đối của NJ và Al là gì? (Chọn một trong các số sau rồi điền vào ở kết quả: 1. Song song. 2. cắt nhau. 3. chéo nhau. 1. cũng năm trên 1 đương thẳng.)
Câu 3: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I, K lần lượt là trung điểm của BC và CD. Gọi M là trung điểm của SB. Gọi F là giao điểm của DM và (SIK). Tình tỉ số MF/MD
Câu 3 :
Ta có : \(S=\left(SIK\right)\cap\left(SAC\right)\left(1\right)\)
Gọi \(E=IK\cap AC\)
\(IK\in\left(SIK\right);AC\in\left(SAC\right)\)
\(\Rightarrow E=\left(SIK\right)\cap\left(SAC\right)\left(2\right)\)
\(\left(1\right);\left(2\right)\Rightarrow SE\in\left(SIK\right)\cap\left(SAC\right)\)
Ta lại có : \(S=\left(SIK\right)\cap\left(SBD\right)\)
mà \(IK\in\left(SIK\right);BD\in\left(SBD\right);IK//BD\) (\(IK\) là đường trung bình \(\Delta BCD\))
\(\Rightarrow Sx=\left(SIK\right)\cap\left(SBD\right)\left(3\right)\) \(\left(Sx//BD//IK\right)\)
Xét \(Mp\left(SBD\right):F=Sx\cap DM\)
\(\Rightarrow S\in DM;S\in Sx\in\left(SIK\right)\)
\(\Rightarrow F=DM\cap\left(SIK\right)\left(4\right)\)
\(\left(3\right);\left(4\right)\Rightarrow SF//BD\)
\(\Rightarrow\dfrac{MF}{MD}=\dfrac{MS}{MB}=1\left(đpcm\right)\) (\(M\) là trung điểm \(SB\))
1.
Gọi E là trung điểm CD \(\Rightarrow G\in SE\) và \(SG=\dfrac{2}{3}SE\) (1) theo t/c trọng tâm
Trong mp (ABCD), nối BE kéo dài cắt AD tại P.
Trong mp (SBE), nối BG kéo dài cắt SP tại H
\(\Rightarrow H=BG\cap\left(SAD\right)\)
Do CD song song AB, áp dụng định lý Thales:
\(\dfrac{PE}{PB}=\dfrac{DE}{AB}=\dfrac{1}{2}\) (do E là trung điểm CD và \(AD=CD\))
\(\Rightarrow PB=2PE\Rightarrow E\) là trung điểm của BP (2)
(1);(2) \(\Rightarrow G\) cũng đồng thời là trọng tâm tam giác SBP
\(\Rightarrow H\) là trung điểm SP
Trong mp (ABCD), gọi F là giao điểm CI và BE
Trong mp (SBE), gọi K là giao điểm BG và SF
\(\Rightarrow K=BG\cap\left(SIC\right)\)
\(2IB=AI=AB-IB\Rightarrow IB=\dfrac{1}{3}AB\)
Áp dụng định lý Thales:
\(\dfrac{FB}{FE}=\dfrac{IB}{CE}=\dfrac{\dfrac{1}{3}AB}{\dfrac{1}{2}CD}=\dfrac{2}{3}\)
\(\Rightarrow3FB=2FE=2\left(BE-FB\right)\Rightarrow FB=\dfrac{2}{5}BE=\dfrac{1}{5}BP=\dfrac{1}{5}\left(FP+FB\right)\)
\(\Rightarrow4FB=FP\Rightarrow\dfrac{FP}{FB}=4\)
Áp dụng định lý Menelaus cho tam giác BPH:
\(\dfrac{SH}{SP}.\dfrac{FP}{FB}.\dfrac{BK}{KH}=1\Leftrightarrow\dfrac{1}{2}.4.\dfrac{BK}{KH}=1\)
\(\Rightarrow\dfrac{BK}{KH}=\dfrac{1}{2}\Rightarrow\dfrac{BK}{BH}=\dfrac{1}{3}\)
2.
\(\dfrac{AM}{AB}=\dfrac{1}{3}\Rightarrow3AM=AB=AM+BM\Rightarrow2AM=BM\Rightarrow\dfrac{AM}{MB}=\dfrac{1}{2}\)
\(AN=3NC\Rightarrow\dfrac{CN}{NA}=\dfrac{1}{3}\)
Đồng thời \(3CN=AN=AC-CN\Rightarrow4CN=CA\Rightarrow\dfrac{CN}{CA}=\dfrac{1}{4}\) (1)
Trong mp (ABC), nối MN cắt BC kéo dài tại E
Trong mp (BCD), nối GE cắt CD tại J
Áp dụng định lý Menelaus cho tam giác ABC:
\(\dfrac{AM}{MB}.\dfrac{BE}{EC}.\dfrac{CN}{NA}=1\Leftrightarrow\dfrac{1}{2}.\dfrac{BE}{EC}.\dfrac{1}{3}=1\Rightarrow BE=6EC\)
Do G là trọng tâm BCD \(\Rightarrow\dfrac{IG}{BG}=\dfrac{1}{2}\)
Áp dụng định lý Menelaus cho tam giác BCI:
\(\dfrac{IG}{GB}.\dfrac{BE}{EC}.\dfrac{CJ}{JI}=1\Leftrightarrow\dfrac{1}{2}.6.\dfrac{CJ}{JI}=1\)
\(\Rightarrow3CJ=IJ=CI-CJ\Rightarrow4CJ=CI\Rightarrow\dfrac{CJ}{CI}=\dfrac{1}{4}\) (2)
(1);(2) \(\Rightarrow\dfrac{CN}{CA}=\dfrac{CJ}{CI}\Rightarrow NJ\) song song \(AI\)
Bài 2 còn 1 cách nữa ngắn gọn hơn:
G là trọng tâm tam giác BCD nên \(\dfrac{BG}{BI}=\dfrac{2}{3}\)
Theo giả thiết \(\dfrac{AM}{AB}=\dfrac{1}{3}\Rightarrow\dfrac{BM}{AB}=\dfrac{2}{3}\)
\(\Rightarrow\dfrac{BG}{BI}=\dfrac{BM}{BA}\Rightarrow MG||AI\)
Ba mặt phẳng (ABI), (ACD), (MNG) cắt nhau theo 3 giao tuyến phân biệt là MG, AI và NJ nên 3 giao tuyến này song song hoặc đồng quy.
Mà MG song song AI theo cmt nên \(MG||AI||NJ\)
Vậy \(NJ\) song song \(AI\). (vị trí điểm N trên AC ko quan trọng, nằm đâu thì nó cũng tạo ra 1 giao tuyến song song AI)