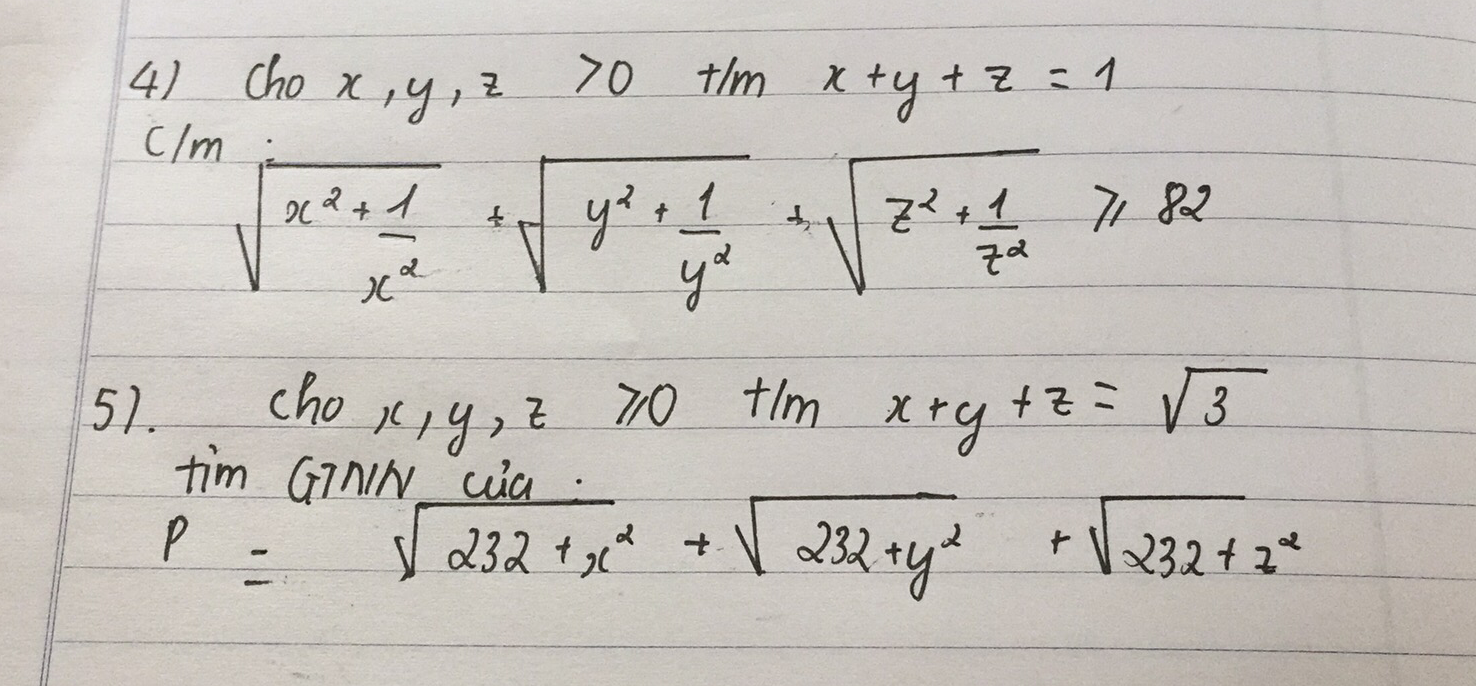4) \(\sqrt{x^2+\dfrac{1}{x^2}}+\sqrt{y^2+\dfrac{1}{y^2}}+\sqrt{z^2+\dfrac{1}{z^2}}\)
\(=\dfrac{1}{\sqrt{82}}.\sqrt{\left(x^2+\dfrac{1}{x^2}\right)\left(1+81\right)}+\dfrac{1}{\sqrt{82}}.\sqrt{\left(y^2+\dfrac{1}{y^2}\right)\left(1+81\right)}+\dfrac{1}{\sqrt{82}}.\sqrt{\left(z^2+\dfrac{1}{z^2}\right)\left(1+81\right)}\)
\(\ge^{Bunhiacopxki}\dfrac{1}{\sqrt{82}}\left[\left(x+\dfrac{9}{x}\right)+\left(y+\dfrac{9}{y}\right)+\left(z+\dfrac{9}{z}\right)\right]\)
\(=\dfrac{1}{\sqrt{82}}.\left[\left(x+\dfrac{1}{9x}\right)+\left(y+\dfrac{1}{9y}\right)+\left(z+\dfrac{1}{9z}\right)+\dfrac{80}{9}\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)\right]\)
\(\ge\dfrac{1}{\sqrt{82}}.\left(2\sqrt{x.\dfrac{1}{9x}}+2\sqrt{y.\dfrac{1}{9y}}+2\sqrt{z.\dfrac{1}{9z}}+\dfrac{80}{9}.\dfrac{9}{x+y+z}\right)\)
\(=\dfrac{1}{\sqrt{82}}.\left(\dfrac{2}{3}+\dfrac{2}{3}+\dfrac{2}{3}+\dfrac{80}{9}.\dfrac{9}{1}\right)\)
\(=\dfrac{1}{\sqrt{82}}.82=\sqrt{82}\)
Dấu "=" xảy ra \(\Leftrightarrow x=y=z=\dfrac{1}{3}\)
5) \(P=\sqrt{232+x^2}+\sqrt{232+y^2}+\sqrt{232+z^2}\)
\(=\dfrac{1}{3\sqrt{697}}.\sqrt{\left(232+x^2\right)\left(6264+9\right)}+\dfrac{1}{3\text{}\text{}\sqrt{697}}.\sqrt{\left(232+y^2\right)\left(6264+9\right)}+\dfrac{1}{3\sqrt{697}}.\sqrt{\left(232+y^2\right)\left(6264+9\right)}\)
\(\ge^{Bunhiacopxki}\dfrac{1}{3\sqrt{697}}.\left[\left(\sqrt{232.6264}+3x\right)+\left(\sqrt{232.6264}+3x\right)+\left(\sqrt{232.6264}+3x\right)\right]\)
\(=\dfrac{1}{3\sqrt{697}}.\left[\left(696\sqrt{3}+3x\right)+\left(696\sqrt{3}+3y\right)+\left(696\sqrt{3}+3z\right)\right]\)
\(=\dfrac{1}{3\sqrt{697}}.\left[3.696\sqrt{3}+3\left(x+y+z\right)\right]\)
\(=\dfrac{1}{3\sqrt{697}}.\left(2088\sqrt{3}+3\sqrt{3}\right)\)
\(=\dfrac{2091\sqrt{3}}{3\sqrt{697}}=\dfrac{697.\sqrt{3}}{\sqrt{697}}=\sqrt{2091}\)
Vậy \(MinP=\sqrt{2091}\), đạt được khi \(x=y=z=\dfrac{\sqrt{3}}{3}\)