Từ phương trình dao động cưỡng bức F=2cos(5πt)
Ta có: \(\omega=10\pi\Rightarrow T=\dfrac{2\pi}{10\pi}=0,2s\)
D/S: \(0,2s\)
Đúng 2
Bình luận (0)
Các câu hỏi tương tự
Một con lắc lò xo có khối lượng 100 g dao động cưỡng bức ổn định dưới tác dụng của ngoại lực biến thiên điều hoà với tần số f. Đồ thị biểu diễn sự phụ thuộc của biên độ vào tần số của ngoại lực tác dụng lên hệ có dạng như hình vẽ. Lấy
π
2
10. Độ cứng của lò xo là A. 25 N/m. B. 42,25 N/m. C. 75 N/m. D. 100 N/m
Đọc tiếp
Một con lắc lò xo có khối lượng 100 g dao động cưỡng bức ổn định dưới tác dụng của ngoại lực biến thiên điều hoà với tần số f. Đồ thị biểu diễn sự phụ thuộc của biên độ vào tần số của ngoại lực tác dụng lên hệ có dạng như hình vẽ. Lấy π 2 = 10. Độ cứng của lò xo là
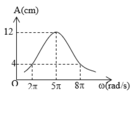
A. 25 N/m.
B. 42,25 N/m.
C. 75 N/m.
D. 100 N/m
Một vật có khối lượng 10 g dao động điều hòa quanh vị trí cân bằng x 0, có đồ thị sự phụ thuộc hợp lực tác dụng lên vật vào li độ như hình vẽ. Chu kì dao động của vật là A. 0,256 s B. 0,152 s C. 0,314 s D. 1,255 s
Đọc tiếp
Một vật có khối lượng 10 g dao động điều hòa quanh vị trí cân bằng x = 0, có đồ thị sự phụ thuộc hợp lực tác dụng lên vật vào li độ như hình vẽ. Chu kì dao động của vật là
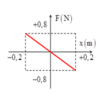
A. 0,256 s
B. 0,152 s
C. 0,314 s
D. 1,255 s
Khảo sát thực nghiệm một con lắc lò xo gồm vật nhỏ có khối lượng 216 g và lò xo có độ cứng k, dao động dưới tác dụng của ngoại lực
F
F
0
cos
2
π
f
t
, với
F
0
không đổi và f thay đổi được. Kết quả khảo sát ta được đường biểu diễn biên độ A của con lắc theo tần số f có đồ thị như hình vẽ. Giá trị của k xấp xỉ bằng A. 13,64 N...
Đọc tiếp
Khảo sát thực nghiệm một con lắc lò xo gồm vật nhỏ có khối lượng 216 g và lò xo có độ cứng k, dao động dưới tác dụng của ngoại lực F = F 0 cos 2 π f t , với F 0 không đổi và f thay đổi được. Kết quả khảo sát ta được đường biểu diễn biên độ A của con lắc theo tần số f có đồ thị như hình vẽ. Giá trị của k xấp xỉ bằng
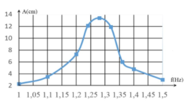
A. 13,64 N/m.
B. 12,35 N/m.
C. 15,64 N/m
D. 16,71 N/m.
Một chất điểm dao động điều hòa có phương trình x=2cos(5πt-π/4) (cm) a) Xác định biên độ, chu kì, tần số và chiều dài quỹ đạo của dao động. b) Viết phương trình vận tốc và gia tốc của chất điểm. c) Tính pha, li độ, vận tốc và gia tốc ở thời điểm t = 0,2 s.
Một vật năng được gắn vào một lò xo có độ cứng 40 N/m thực hiện dao động cưỡng bức. Sự phụ thuộc của biên độ dao động này vào tần số của lực cưỡng bức được biểu diễn như hình vẽ. Hãy xác định năng lượng toàn phần của hệ khi cộng hưởng A. 5.
10
-
2
J
B.
10
-
2
J
C. 1,25.
10...
Đọc tiếp
Một vật năng được gắn vào một lò xo có độ cứng 40 N/m thực hiện dao động cưỡng bức. Sự phụ thuộc của biên độ dao động này vào tần số của lực cưỡng bức được biểu diễn như hình vẽ. Hãy xác định năng lượng toàn phần của hệ khi cộng hưởng

A. 5. 10 - 2 J
B. 10 - 2 J
C. 1,25. 10 - 2 J
D. 2. 10 - 2 J
1 vật dao động điều hòa với chu kì = 2s, A = 4cm, tại thời điểm t, vật có li độ tốc độ v = 2\(\pi\) cm/s thì vật cách vị trí cân bằng 1 khoảng bằng bao nhiêu
1) 1 dao động điều hòa với phương trình v3pi cosleft(pi tright)cm/s. xác định tốc độ cực đại, tần số góc, chu kì, tần số, pha ban đầu và tính vận tốc tại thời điểm t 3s2) một vật dao động điều hòa có phương trình gia tốc a4pi^2cosleft(pi t-dfrac{pi}{2}right)xác định gia tốc cực đại, tần số góc, chu kì và pha ban đầu của gia tốc
Đọc tiếp
1) 1 dao động điều hòa với phương trình \(v=3\pi cos\left(\pi t\right)\)cm/s. xác định tốc độ cực đại, tần số góc, chu kì, tần số, pha ban đầu và tính vận tốc tại thời điểm t = 3s
2) một vật dao động điều hòa có phương trình gia tốc \(a=4\pi^2cos\left(\pi t-\dfrac{\pi}{2}\right)\)xác định gia tốc cực đại, tần số góc, chu kì và pha ban đầu của gia tốc
một con lắc lò xo gồm vật nặng có khối lượng 10g gắn với lò xo có độ cứng 10N/m dao động điều hòa trên mặt sàn nhẵn nằm ngang với phương trình x10cos ωt (cm), vào thời điểm t vật chịu tác dụng của lực F hướng dọc theo trục của lò xo và có độ lớn không đổi F0,6N sau thời điểm đó vật dao động trên quỹ đạo có chiều dài 16cm. Vật bắt đầu chịu tác dụng của lực F khi nó cách gốc O một khoảng bằng?A. 8cm B. 6cmC. 4cm D. 5cm
Đọc tiếp
một con lắc lò xo gồm vật nặng có khối lượng 10g gắn với lò xo có độ cứng 10N/m dao động điều hòa trên mặt sàn nhẵn nằm ngang với phương trình x=10cos ωt (cm), vào thời điểm t vật chịu tác dụng của lực F hướng dọc theo trục của lò xo và có độ lớn không đổi F=0,6N sau thời điểm đó vật dao động trên quỹ đạo có chiều dài 16cm. Vật bắt đầu chịu tác dụng của lực F khi nó cách gốc O một khoảng bằng?
A. 8cm
B. 6cm
C. 4cm
D. 5cm
1 vật dao động điều hòa với A = 20cm khi li độ là 10cm thì vận tốc của vật là \(20\pi\sqrt{3}\) cm/s. Tính chu kì của vật dao động
Một con lắc lò xo treo thẳng đứng gồm lò xo nhẹ có độ cứng k gắn với vật nhỏ có khối lượng m đang dao động điều hòa. Lực đàn hồi của lò xo tác dụng lên vật trong quá trình dao động có đồ thị như hình vẽ. Thời gian lò xo bị nén trong một chu kì là A.
2
π
3
m
k
B.
π
6...
Đọc tiếp
Một con lắc lò xo treo thẳng đứng gồm lò xo nhẹ có độ cứng k gắn với vật nhỏ có khối lượng m đang dao động điều hòa. Lực đàn hồi của lò xo tác dụng lên vật trong quá trình dao động có đồ thị như hình vẽ. Thời gian lò xo bị nén trong một chu kì là
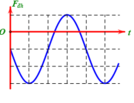
A. 2 π 3 m k
B. π 6 m k
C. π 3 m k
D. 4 π 3 m k







