\(W=\dfrac{1}{2}CU^2=\dfrac{1}{2}.2000.10^{-6}.10^2=0,1\left(J\right)\)
tham khảo
Công thức tính năng lượng điện trường: \(W=\dfrac{1}{2}CU^2=\dfrac{1}{2}2000.10^{-6}.10^2=0,1J\)
\(W=\dfrac{1}{2}CU^2=\dfrac{1}{2}.2000.10^{-6}.10^2=0,1\left(J\right)\)
tham khảo
Công thức tính năng lượng điện trường: \(W=\dfrac{1}{2}CU^2=\dfrac{1}{2}2000.10^{-6}.10^2=0,1J\)
Cho các dụng cụ sau:
Một tụ điện có điện dung 100 µF và hiệu điện thế định mức khoảng 12 V; 4 pin 1,5 V; Một LED; Một điện trở 50 Ω; công tắc, dây dẫn điện. Nêu phương án dùng các dụng cụ này chứng minh tụ điện có lưu trữ năng lượng.
Vì sao tụ điện có năng lượng?
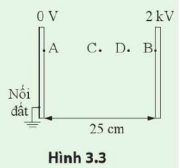
Cho hai bản cực song song, cách nhau 25 cm như hình 3.3. Hiệu điện thế giữa hai bản là 2 kV.
a) Hiệu điện thế giữa hai điểm A và B là bao nhiêu?
b) Cường độ điện trường tại C và tại D là bao nhiêu?
c) Tìm lực điện tác dụng lên một điện tích +5 µC đặt tại C.
Để dịch chuyển một điện tích dương đến gần điện tích dương khác, cần phải đẩy nó để thắng lực đẩy giữa chúng, Hình 3.1. Trong trường hợp này, ta nói rằng cần phải thực hiện một công để di chuyển một điện tích lại gần một điện tích khác.
Năng lượng của một điện tích di chuyển trong điện trường được xác định như thế nào?

Vì sao thế năng của điện tích tăng theo chiều ngược với chiều của cường độ điện trường?
Vì sao đường biểu diễn sự thay đổi thế năng điện trong điện trường đều ở Hình 3.2 là một đường thẳng?

So sánh công của lực điện dịch chuyển một đơn vị điện tích dương từ điểm đang xét ra vô cùng và công thực hiện để dịch chuyển một đơn vị điện tích dương từ vô cùng về điểm đang xét.
Điện thế tại một điểm trong điện trường là gì?