Các câu hỏi tương tự
cho tam giác ABC cân tại A, cạnh bên dài 8 cm , 1 đường thẳng song song với BC cắt AB và AC tại D và E. Biết chu vi BDEC là 11 cm. Tính chu vi tam giác ADE
Cho tam giác ABC vuông ở A. Cạnh AB dài 30 cm, cạnh AC dài 40cm. Trên cạnh BC lấy trung điểm D, trên cạnh AB lấy điểm E sao cho AE=\(\frac{1}{3}\)AB. Nối AD cắt CE tại M.
Tính tỉ số diện tích tam giác AME và diện tích tam giác ABC
Cho tam giác ABC vuông tại A, có AB=5cm và BC=10cm. Gọi M, N, P lần lượt là trung điểm
của các cạnh AB, BC, CA. Chu vi đường tròn ngoại tiếp tam giác MNP là ......?..cm
(Nhập kết quả dưới dạng số thập phân làm tròn đến 1 chữ số sau dấu “,”)
Cho tam giác ABC vuông tại A có AB= 9cm ; BC=10cm
a. Tính AC và so sánh các góc tam giác ABC
b. Trên tia đối tia AB lấy điểm D sao cho A là trung điểm BD. Chứng minh tam giác BCD cân
c. Gọi E; F lần lượt là trung điểm các cạnh DC, BC. Đường thẳng BE cắt cạnh AC tại M.
Tính CM và chứng minh 3 điểm D; M; F thẳng hàng
Cho tam giác ABC vuông tại A có
B
C
2
a
v
à
A
B
C
⏜
30
∘
. Quay tam giác vuông này quanh cạnh AB, ta được một hình nón đỉnh B. Gọi
S
1
là diện tích xung quanh của hình nón đó và
S
2
là diện tích mặ...
Đọc tiếp
Cho tam giác ABC vuông tại A có B C = 2 a v à A B C ⏜ = 30 ∘ . Quay tam giác vuông này quanh cạnh AB, ta được một hình nón đỉnh B. Gọi S 1 là diện tích xung quanh của hình nón đó và S 2 là diện tích mặt cầu có đường kính AB. Khi đó, tỉ số S 1 S 2 là
A. S 1 S 2 = 1
B. S 1 S 2 = 2 3
C. S 1 S 2 = 1 2
D. S 1 S 2 = 3 2
Cho hình lăng trụ đứng tam giác ABC.ABC có đáy ABC là tam giác cân, ABACa,
B
A
C
^
120
∘
, cạnh bên
A
A
a
2
. Tính góc giữa hai đường thẳng AB và BC. (tham khảo hình vẽ bên) A.
90
∘
B.
30
∘
C. ...
Đọc tiếp
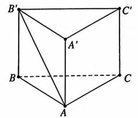
Cho hình lăng trụ đứng tam giác ABC.A'B'C' có đáy ABC là tam giác cân, AB=AC=a, B A C ^ = 120 ∘ , cạnh bên A A ' = a 2 . Tính góc giữa hai đường thẳng AB' và BC. (tham khảo hình vẽ bên)
A. 90 ∘
B. 30 ∘
C. 45 ∘
D. 60 ∘
Cho tứ diện ABCD có tam giác ABD đều là cạnh bằng 2, tam giác ABC vuông tại B,
B
C
3
. Biết khoảng cách giữa hai đường thẳng chéo nhau AB và CD bằng
11
2
. Khi đó độ dài cạnh CD là A. 2 B. 1 C.
3
D.
2
Đọc tiếp
Cho tứ diện ABCD có tam giác ABD đều là cạnh bằng 2, tam giác ABC vuông tại B, B C = 3 . Biết khoảng cách giữa hai đường thẳng chéo nhau AB và CD bằng 11 2 . Khi đó độ dài cạnh CD là
A. 2
B. 1
C. 3
D. 2
Cho tam giác ABC vuông tại A. Các cạnh AB, AC, BC của hình tam giác lần lượt là 3; 4; 5. Tính thể tích hình nón khi quay tam giác quanh trục AB
A. 12 π
B. 16 π
C. 48 π
D. Đ á p á n k h á c
Cho tam giác ABC với trọng tâm G. Gọi A’, B’, C’ lần lượt là trung điểm của các cạnh BC, AC, AB của tam giác ABC. Khi đó phép vị tự nào biến tam giác A’B’C thành tam giác ABC? A. Phép vị tự tâm G, tỉ số -1/2 B. Phép vị tự tâm G, tỉ số 1/2 C. Phép vị tự tâm G, tỉ số 2 D. Phép vị tự tâm G, tỉ số -2
Đọc tiếp
Cho tam giác ABC với trọng tâm G. Gọi A’, B’, C’ lần lượt là trung điểm của các cạnh BC, AC, AB của tam giác ABC. Khi đó phép vị tự nào biến tam giác A’B’C thành tam giác ABC?
A. Phép vị tự tâm G, tỉ số -1/2
B. Phép vị tự tâm G, tỉ số 1/2
C. Phép vị tự tâm G, tỉ số 2
D. Phép vị tự tâm G, tỉ số -2







