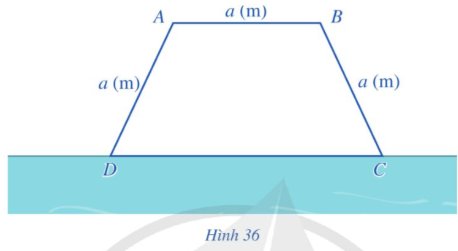
Giả sử chiều dài của hai cạnh đáy của hình thang cân lần lượt là \(x\) và \(2x\), và chiều dài của cạnh bên là \(a - 3x\). Do đó, chiều cao của hình thang cân là: \(h = \sqrt {{{(a - 3x)}^2} - {x^2}} \)
Diện tích của hình thang cân là:
\(S = \frac{{\left( {x + 2x} \right)h}}{2} = \frac{{3x\sqrt {{{(a - 3x)}^2} - {x^2}} }}{2}\)
Để tìm giá trị lớn nhất của S, ta cần tìm giá trị x sao cho đạo hàm của S theo x bằng 0. Đạo hàm của S theo x được tính bằng công thức sau:
\(S' = \frac{{dS}}{{dx}} = \frac{{3x\left( {8x - 9} \right)}}{{2\sqrt { - {x^2} + {{(a - 3x)}^2}} }} + \frac{{3\sqrt { - {x^2} + {{(a - 3x)}^2}} }}{2}\).
Giải phương trình \(S' = 0\)
Sau khi giải, thay x vào công thức diện tích S, ta tìm được diện tích lớn nhất của mảnh vườn có thể rào được là \({S_{max}} = \frac{{{a^2}\sqrt 3 }}{4}\)