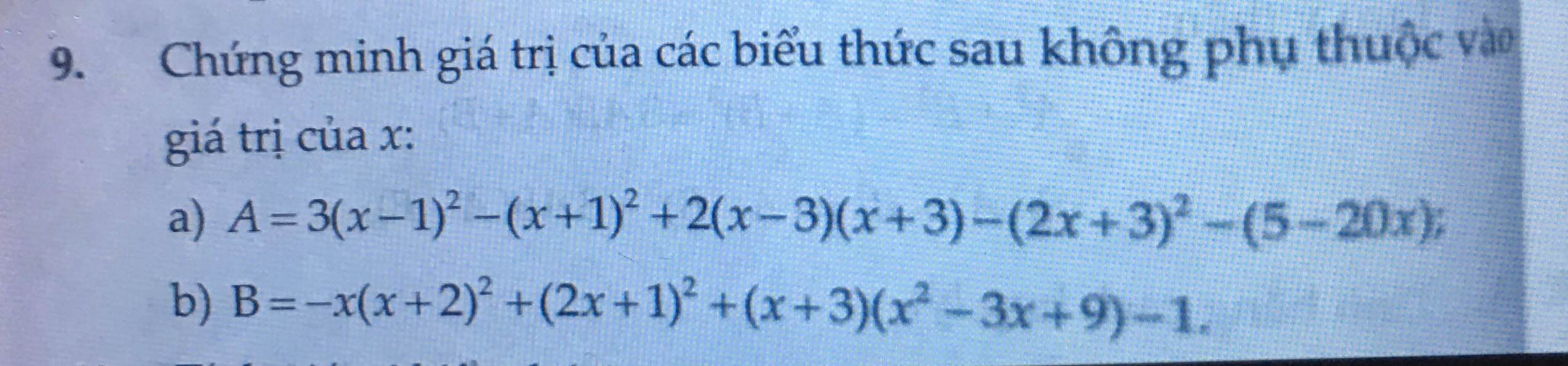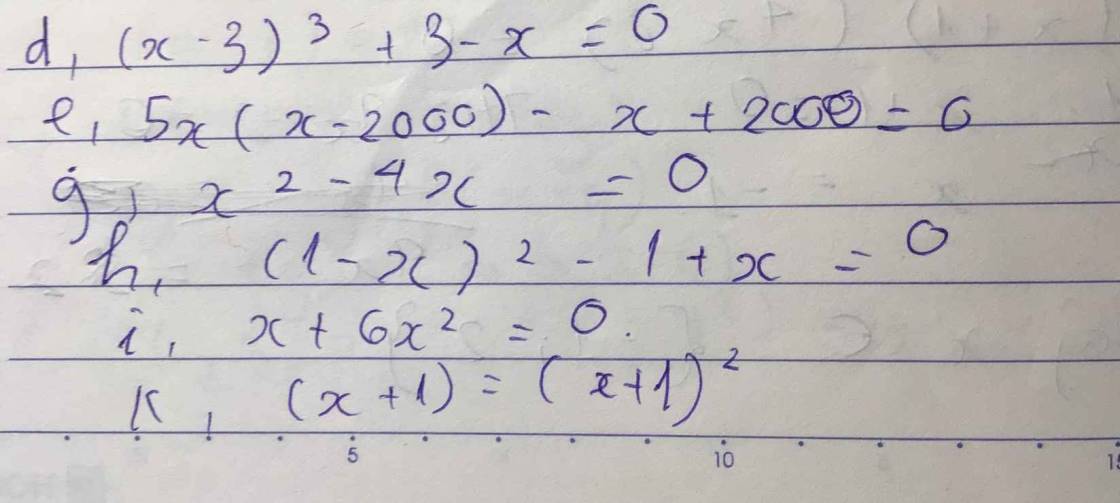Question

mọi người ơi giúp mình với mình phải nộp luôn rồi mà khó quá :((((

Answer 1

Bài 1:

$x^3+y^3\geq xy(x+y)$

$\Leftrightarrow x^3+y^3-x^2y-xy^2\geq 0$

$\Leftrightarrow (x^3-x^2y)-(xy^2-y^3)\geq 0$

$\Leftrightarrow x^2(x-y)-y^2(x-y)\geq 0$

$\Leftrightarrow (x-y)(x^2-y^2)\geq 0$

$\Leftrightarrow (x-y)^2(x+y)\geq 0$ (luôn đúng với mọi $x,y\geq 0$)

Do đó BĐT được chứng minh

Dấu "=" xảy ra khi $x=y$

Answer 2

Bài 2:

Áp dụng BĐT AM-GM:

$\frac{a^2}{b}+b\geq 2a$

$\frac{b^2}{c}+c\geq 2b$

$\frac{c^2}{a}+a\geq 2c$

Cộng các BĐT trên theo vế và thu gọn ta có:
$\frac{a^2}{b}+\frac{b^2}{c}+\frac{c^2}{a}\geq a+b+c$ (đpcm)

Dấu "=" xảy ra khi $a=b=c$

Answer 3

Bải 3:

1. 

Do $a,b,c$ là độ dài 3 cạnh tam giác nên theo BĐT tam giác thì:

$a< b+c\Rightarrow a^2< a(b+c)$

Tương tự: $b^2< b(c+a)$; $c^2<c(a+b)$

Cộng theo vế các BĐT trên thì:

$a^2+b^2+c^2< 2(ab+bc+ac)$ (đpcm)

2.

Áp dụng BĐT AM-GM:

$(a+b-c)(b+c-a)\leq \left(\frac{a+b-c+b+c-a}{2}\right)^2=b^2$
$(b+c-a)(a+c-b)\leq \left(\frac{b+c-a+a+c-b}{2}\right)^2=c^2$
$(a+b-c)(a+c-b)\leq \left(\frac{a+b-c+a+c-b}{2}\right)^2=a^2$
Nhân theo vế các BĐT trên và thu gọn ta được:

$(a+b-c)(b+c-a)(c+a-b)\leq abc$ (đpcm)

Dấu "=" xảy ra khi $a=b=c$

Answer 4

Bài 4:

Do $a+b+c=0$ nên $c=-a-b$

Khi đó:

$ab+2bc+3ac=ab+2b(-a-b)+3a(-a-b)=ab-2ab-2b^2-3a^2-3ab=-3a^2-2b^2-4ab$

$=-a^2-2(a^2+b^2+2ab)=-a^2-2(a+b)^2=-[a^2+(a+b)^2]\leq 0$ với mọi $a,b$

$\Rightarrow$ đpcm

 

Answer 5

Bài 5:

CM vế đầu tiên:

Áp dụng BĐT Bunhiacopxky:

$(a^2+b^2+c^2)(1+1+1)\geq (a+b+c)^2$

$\Leftrightarrow a^2+b^2+c^2\geq \frac{(a+b+c)^2}{3}=\frac{3^2}{3}=3$

Ta có đpcm

Dấu "=" xảy ra khi $a=b=c=1$

----------------------

Chứng minh vế thứ hai

Vì $a,b,c\in [0;2]$ nên:

$(a-2)(b-2)(c-2)\leq 0$

$\Leftrightarrow (ab-2a-2b+4)(c-2)\leq 0$

$\Leftrightarrow abc-2(ab+bc+ac)+4(a+b+c)-8\leq 0$

$\Leftrightarrow abc-2(ab+bc+ac)+4\leq 0$

$\Leftrightarrow 2(ab+bc+ac)\geq abc+4\geq 4$ (do $abc\geq 0$)

Khi đó:

$a^2+b^2+c^2=(a+b+c)^2-2(ab+bc+ac)=9-2(ab+bc+ac)\leq 9-4=5$

(đpcm)

Dấu "=" xảy ra khi $(a,b,c)=(0,1,2)$ và hoán vị/

Answer 6

Bài 6:

BĐT cần chứng minh tương đương với:

$\frac{x^2+y^2+2}{(1+x^2)(1+y^2)}\geq \frac{2}{1+xy}$

$\Leftrightarrow (x^2+y^2+2)(xy+1)\geq 2(1+x^2)(1+y^2)$

$\Leftrightarrow x^3y+x^2+xy^3+y^2+2xy+2\geq 2+2x^2+2y^2+2x^2y^2$

$\Leftrightarrow x^3y+xy^3+2xy\geq x^2+y^2+2x^2y^2$

$\Leftrightarrow xy(x^2+y^2-2xy)-(x^2+y^2-2xy)\geq 0$

$\Leftrightarrow xy(x-y)^2-(x-y)^2\geq 0$

$\Leftrightarrow (x-y)^2(xy-1)\geq 0$ (luôn đúng với mọi $xy\geq 1$)

Do đó ta có đpcm.