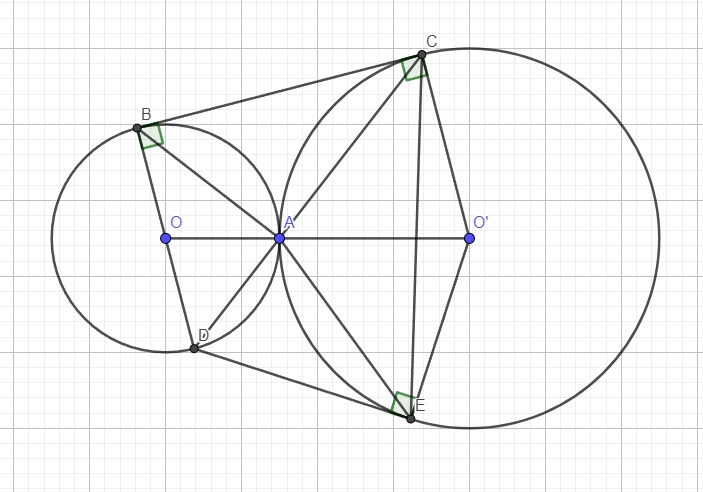
MỌI NGƯỜI GIÚP MÌNH CÂU 5C VỚI Ạ. MÌNH CẢM ƠN. Cho hai đtron (O) và (O') tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài BC, B thuộc (O), C thuộc (O'). Đường thẳng BO cắt (O) tại điểm thứ hai tại D.
a. CMR: Tứ giác CO'OB là hthang vuông.
b. CMR: Ba điển A,C,D thẳng hàng.
c. Từ D kẻ tiếp tuyến DE với dtron (O') (E là tiếp điểm. CMR: DB=DE
c.
BD là đường kính nên \(\widehat{BAD}=90^0\) (góc nt chắn nửa đường tròn)
BC là tiếp tuyến của (O) nên \(\widehat{DBC}=90^0\)
Xét 2 tam giác BAD và CBD có:
\(\left\{{}\begin{matrix}\widehat{BDA}-chung\\\widehat{BAD}=\widehat{CBD}=90^0\end{matrix}\right.\)
\(\Rightarrow\Delta BAD\sim\Delta CBD\left(g.g\right)\Rightarrow\dfrac{BD}{CD}=\dfrac{AD}{BD}\Rightarrow BD^2=AD.CD\) (1)
Xét hai tam giác DAE và DEC có:
\(\left\{{}\begin{matrix}\widehat{ADE}-chung\\\widehat{DEA}=\widehat{DCE}\left(\text{cùng chắn AE}\right)\end{matrix}\right.\)
\(\Rightarrow\Delta DAE\sim\Delta DEC\left(g.g\right)\Rightarrow\dfrac{DE}{CD}=\dfrac{AD}{DE}\Rightarrow DE^2=AD.CD\) (2)
(1);(2) \(\Rightarrow BD^2=DE^2\Rightarrow BD=DE\)