Mọi người giúp em với em đang cần gấp ạ mai em phải nộp rồi. 1) Cho PT : \(x^2 - 2(m+1)x + m^2 + 2 = 0\), với m là tham số. Tìm m để PT có 2 nghiệm phân biệt x1,x2 thỏa mãn x1^3 - 3x2^2= 2(\(m^2\)+x1x2-1). 2) Một người đứng quan sát ở vị trí A trên nóc 1 ngôi nhà cao 4m đang quan sát một cây cao, cách ngôi nhà 20m và đo đc góc BAC = \(45^0\) ( tham khảo hình vẽ). Tính chiều cao của cây đó (theo đơn vị mét, làm tròn kết quả đến hàng phần mười), biết rằng nếu góc \(\alpha\) nhọn và thỏa mãn tan \(\alpha\) = \(\dfrac{1}{5}\) thì ta chọn \(\alpha\) = \(11^0\). 3) Cho tam giác ABC nhọn có AB < AC, các đg cao BD và CE cắt nhau tại H. a) Cm tứ giác ADHE nội tiếp. ( VẼ HÌNH HỘ EM NHA ) b) Gọi m là trung điểm của BC, đường thẳng DE cắt BC tại N, AH cắt BC tại K. Cmr : góc DEK = góc DMC và NH vuông góc AM
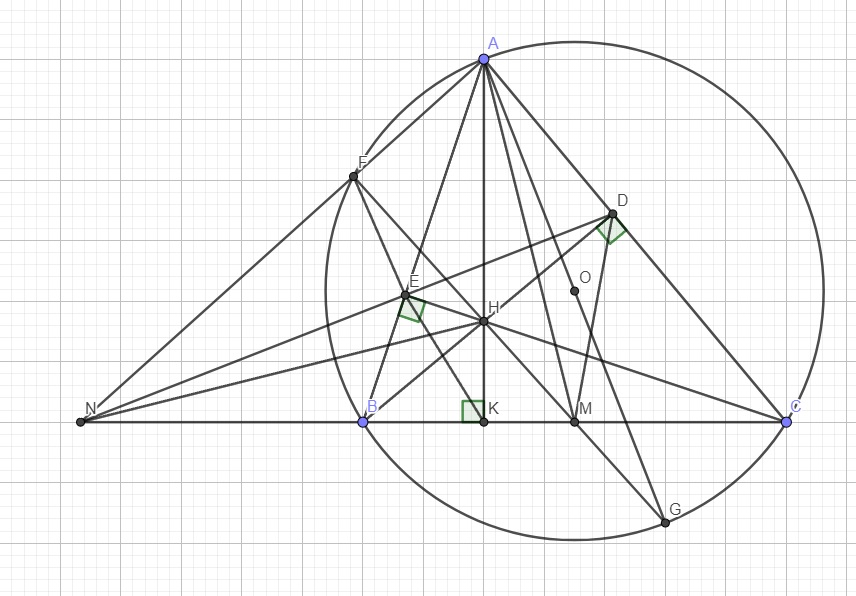
Chứng minh NH vuông góc AM:
Kẻ đường kính AG của đường tròn ngoại tiếp tam giác ABC. Gọi F là giao của AN là đường tròn ngoại tiếp ABC.
\(\Rightarrow\widehat{ACG}\) là góc nt chắn nửa đường tròn \(\Rightarrow\widehat{ACG}=90^0\)
\(\Rightarrow CG\perp AC\) \(\Rightarrow CG||BH\) (cùng vuông góc AC)
Hoàn toàn tương tự ta có \(BG||CH\) (cùng vuông góc AB)
\(\Rightarrow BHCG\) là hình bình hành (2 cặp canh đối song song)
\(\Rightarrow BC;HG\) cắt nhau tại trung điểm mỗi đường
Mà M là trung điểm BC \(\Rightarrow M\in HG\)
BCDE nội tiếp \(\Rightarrow\widehat{NCD}+\widehat{BED}=180^0\)
Mà \(\widehat{BED}+\widehat{NEB}=180^0\) (kề bù)
\(\Rightarrow\widehat{NCD}=\widehat{NEB}\)
Xét hai tam giác NCD và NEB có:
\(\left\{{}\begin{matrix}\widehat{CND}-chung\\\widehat{NCD}=\widehat{NEB}\end{matrix}\right.\) \(\Rightarrow\Delta NCD\sim\Delta NEB\left(g.g\right)\)
\(\Rightarrow\dfrac{NC}{NE}=\dfrac{ND}{NB}\Rightarrow NB.NC=NE.ND\)
Tương tự AFBC nội tiếp nên \(\widehat{NBF}=\widehat{NAC}\) (cùng bù \(\widehat{FBC}\))
\(\Rightarrow\Delta NBF\sim\Delta NAC\Rightarrow\dfrac{NB}{NA}=\dfrac{NF}{NC}\Rightarrow NB.NC=NA.NF\)
\(\Rightarrow NE.ND=NA.NF\Rightarrow\dfrac{NE}{NA}=\dfrac{NF}{ND}\)
Xét hai tam giác NEF và NAD có: \(\left\{{}\begin{matrix}\widehat{N}-chung\\\dfrac{NE}{NA}=\dfrac{NF}{ND}\end{matrix}\right.\)
\(\Rightarrow\Delta NEF\sim\Delta NAD\left(c.g.c\right)\Rightarrow\widehat{NEF}=\widehat{NAD}\)
Mà \(\widehat{NEF}+\widehat{DEF}=180^0\Rightarrow\widehat{NAD}+\widehat{DEF}=180^0\)
\(\Rightarrow ADEF\) nội tiếp
Kết hợp câu a \(\Rightarrow A,D,H,E,F\) cùng thuộc 1 đường tròn
\(\Rightarrow\widehat{AFH}=\widehat{AEH}=90^0\)
\(\Rightarrow AF\perp HF\) (1)
Lại có \(\widehat{AFG}=90^0\) (góc nt chắn nửa đường tròn) \(\Rightarrow AF\perp GF\) (2)
(1);(2) \(\Rightarrow H,G,F\) thẳng hàng \(\Rightarrow HG\perp AF\)
Mà M thuộc HG theo cmt \(\Rightarrow MH\perp AF\)
Trong tam giác ANM, ta có 2 đường cao MF và AK cắt nhau tại H
\(\Rightarrow H\) là trực tâm tam giác ANM
\(\Rightarrow NH\) là đường cao thứ 3
\(\Rightarrow NH\perp AM\)
Làm bài hình thôi nhé, dài ngán quá:
a.
Do E và D cùng nhìn AD dưới 1 góc vuông \(\Rightarrow ADHE\) nội tiếp
b.
H là giao điểm 2 đường cao BE, CE nên H là trực tâm tam giác ABC
\(\Rightarrow AK\) là đường cao thứ 3 \(\Rightarrow AK\perp BC\)
D và E cùng nhìn BC dưới 1 góc vuông \(\Rightarrow BEDC\) nội tiếp đường tròn đường kính BC
Mà M là trung điểm BC \(\Rightarrow M\) là tâm đường tròn ngoại tiếp BEDC
Ta có: \(\widehat{DME}=2\widehat{DBE}\) (góc nt và góc ở tâm cùng chắn DE) (1)
E và K cùng nhìn BH dưới 1 góc vuông \(\Rightarrow BEHK\) nội tiếp
\(\Rightarrow\widehat{DBE}=\widehat{EKH}\) (cùng chắn EH)
D và K cùng nhìn AB dưới 1 góc vuông \(\Rightarrow ABKD\) nội tiếp
\(\Rightarrow\widehat{DBE}=\widehat{DKA}\) (cùng chắn AD)
\(\Rightarrow\widehat{EKH}=\widehat{DKA}=\widehat{DBE}\)
Mà \(\widehat{EKH}+\widehat{DKA}=\widehat{DKE}\)
\(\Rightarrow\widehat{DKE}=2\widehat{DBE}\) (2)
(1);(2) \(\Rightarrow\widehat{DKE}=\widehat{DME}\)
Mà K, M cùng nằm về 1 nửa mp bờ DE \(\Rightarrow DEKM\) nội tiếp
\(\Rightarrow\widehat{DEK}+\widehat{DMK}=180^0\)
Mà \(\widehat{DMK}+\widehat{DMC}=180^0\) (kề bù)
\(\Rightarrow\widehat{DEK}=\widehat{DMC}\) (đpcm)
Ý sau còn dài gấp đôi.