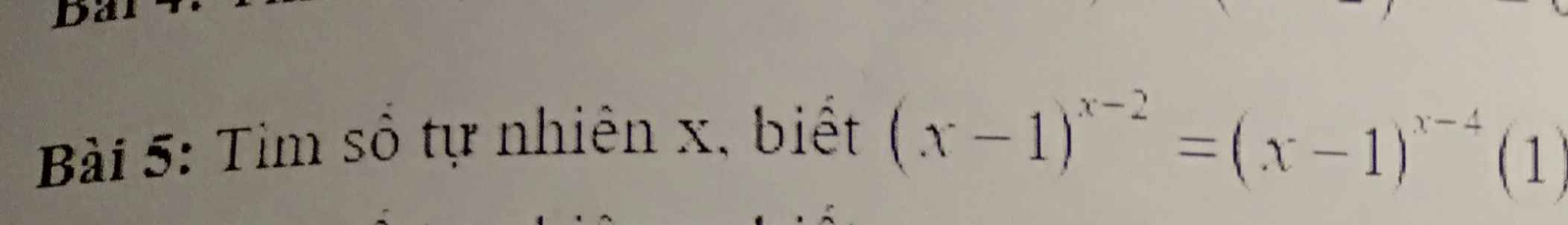Question

Mọi người giúp em bài này nha

Answer 1

Lời giải:
$(x-1)^{x-2}=(x-1)^{x-4}$

$(x-1)^{x-2}-(x-1)^{x-4}=0$

$(x-1)^{x-4}[(x-1)^2-1]=0$

$\Rightarrow (x-1)^{x-4}=0$ hoặc $(x-1)^2-1=0$

Với $(x-1)^{x-4}=0\Rightarrow x=1$. Tuy nhiên khi đó số mũ $x-4=1-4=-3< 0$ nên loại 

Với $(x-1)^2-1=0$

$\Rightarrow x-1=\pm 1\Rightarrow x=2$ hoặc $x=0$ (tm)