đặt cosx=t
x∈ (0;\(\dfrac{\pi}{2}\)) => t∈(0,1)
bài toán trở thành tìm m để y= \(\dfrac{2t-1}{t-m}\)nghịch biến trên (0,1)
hs NB <=> y' <0 <=> -2m+1<0 => m > 1/2 (*)
xét đk: t-m≠0 => m≠t => m∉ (0,1) => \(\begin{matrix}m\le0\\m\ge1\end{matrix}\) (**)
kết hợp (*)(**) \(\begin{matrix}m\le0\\m\ge1\end{matrix}\)
mọi người giải dùm em vs ạ bạn em nhờ em hỏi dùm
em cảm ơn nhiều
Mọi người cho mình hỏi đk bài toán là m<0 , đại loại trong bài có đoạn (\(\sqrt{-m}.\sqrt{-m}\)
em nghĩ là ra -m bởi m<0 thì -m>0 và căn nhân căn thì dương , nhưng gv của em lại bảo là ra m :((( mong mọi người giải đáp hộ em . Em cảm ơn !
mọi người giải thích giùm mình sao đáp án lại ra (0; +dương vô cùng)
Đề bài: Tìm các khoảng đồng biến của hàm số y= x4 + 8x2 + 14
có thể giải thích giúp em tại sao tập xác định của hs y có D =x^2 -x+12 > 0 với mọi x thuộc R mà không phải là D =x^2 -x+12 >= 0 với mọi x thuộc R ạ
Mn cho em xin lời giải bài này ạ..... Em cảm ơn mn nhiều ạ
Thầy ơi , cho em hỏi bài với ạ ! Em vẫn băn khoăn không hiểu vì sao: Điều kiện đơn điệu của hàm bậc 3 là y' >= 0, trong khi đó hàm phân thức lại chỉ là y' > 0 thôi ạ. Em cảm ơn! Các bạn biết thì chỉ giúp mình nhé, Cảm ơn nhiều !
Mn đi qua, cho em xin lời giải với ạ!!!! Em cảm ơn mn nhiều.
Bạn nào giúp mình phần b với ạ. Đáp án giải vắn tắt nên mình không hiểu cho lắm.
1, Chứng minh bất đẳng thức:
\(a+\sqrt{a^2-2a+5}+\sqrt{a-1}\ge3\forall a\ge1\)
2, Giải phương trình:
\(x\left(x^2-3x+3\right)+\sqrt{x+3}=3\)
Mong mọi người giúp mình với ạ!! Mình cảm ơn nhiều!!
Mọi người cho e hỏi là tại sao hàm số đồng biến trên (a; +∞) thì hai nghiệm đều nhỏ hơn a ạ
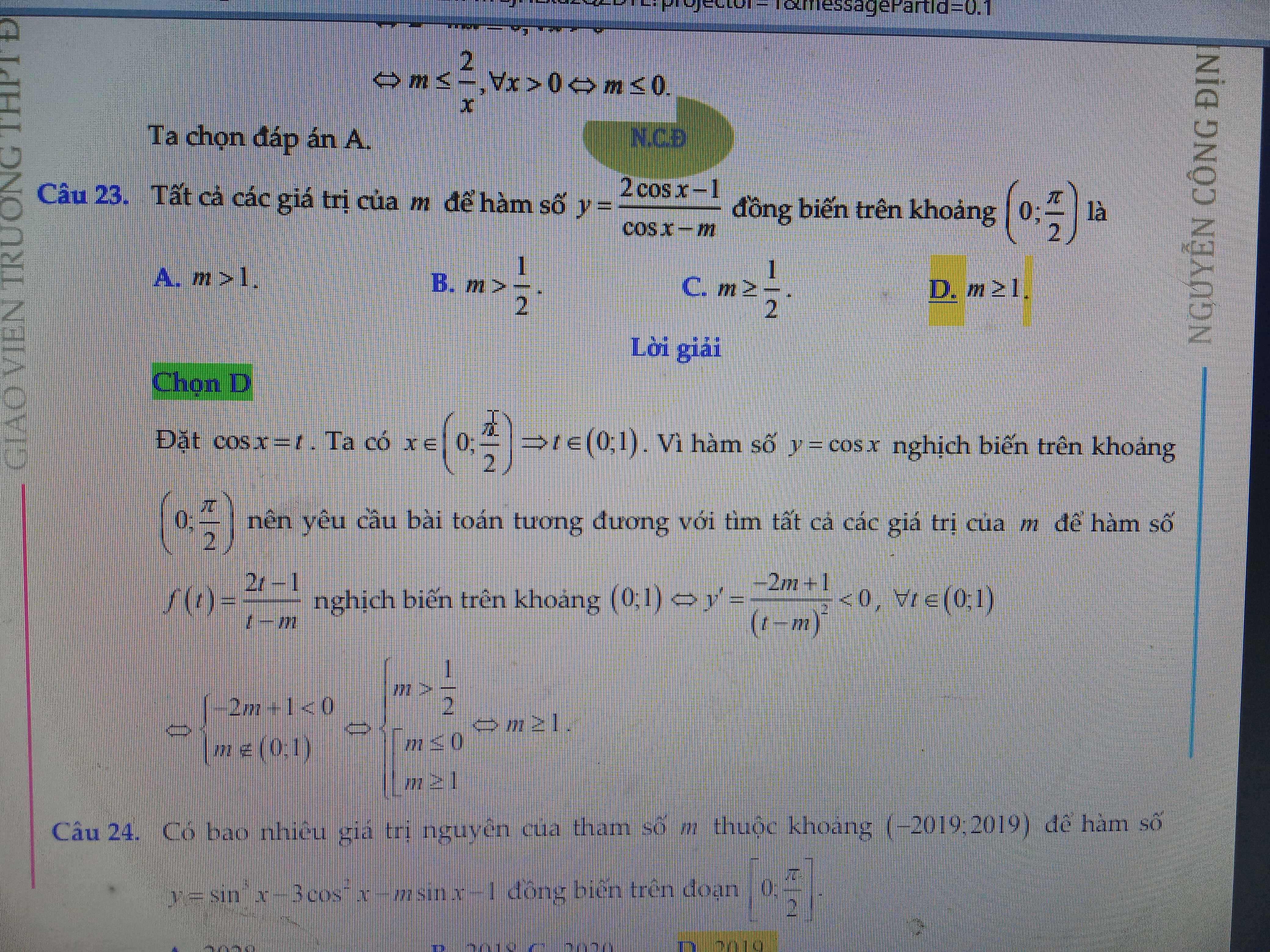Mọi người cho em hỏi tại sao đề bài bắt tìm đồng biến trên khoảng (0,1) mà lời giải lại nêu f'(t)<0 vậy ạ? Nếu giải theo f'(t)>0 lại không ra đáp án đúng vậy ạ? Mong mọi người giải đáp ạ!!! Em cảm ơn!!!
