b) \(=\left(5+2\sqrt{3}\right).\sqrt{25-2.5.2\sqrt{3}+12}\\ =\left(5+2\sqrt{3}\right).\sqrt{\left(5-2\sqrt{3}\right)^2}=\left(5+2\sqrt{3}\right).\left(5-2\sqrt{3}\right)=25-12=13\)
c: \(\left(2-\dfrac{5-\sqrt{5}}{1-\sqrt{5}}\right)\left(\dfrac{\sqrt{10}+\sqrt{5}}{\sqrt{2}+1}-2\right)\)
\(=\left(\sqrt{5}+2\right)\left(\sqrt{5}-2\right)\)
=1
\(b,=\left(5+2\sqrt{3}\right)\sqrt{\left(5-2\sqrt{3}\right)^2}=\left(5+2\sqrt{3}\right)\left(5-2\sqrt{3}\right)=25-12=13\\ c,=\left(2-\dfrac{\sqrt{5}\left(\sqrt{5}-1\right)}{1-\sqrt{5}}\right)\left(\dfrac{\sqrt{5}\left(\sqrt{2}+1\right)}{\sqrt{2}+1}-2\right)\\ =\left(2+\sqrt{5}\right)\left(\sqrt{5}-2\right)=5-4=1\)













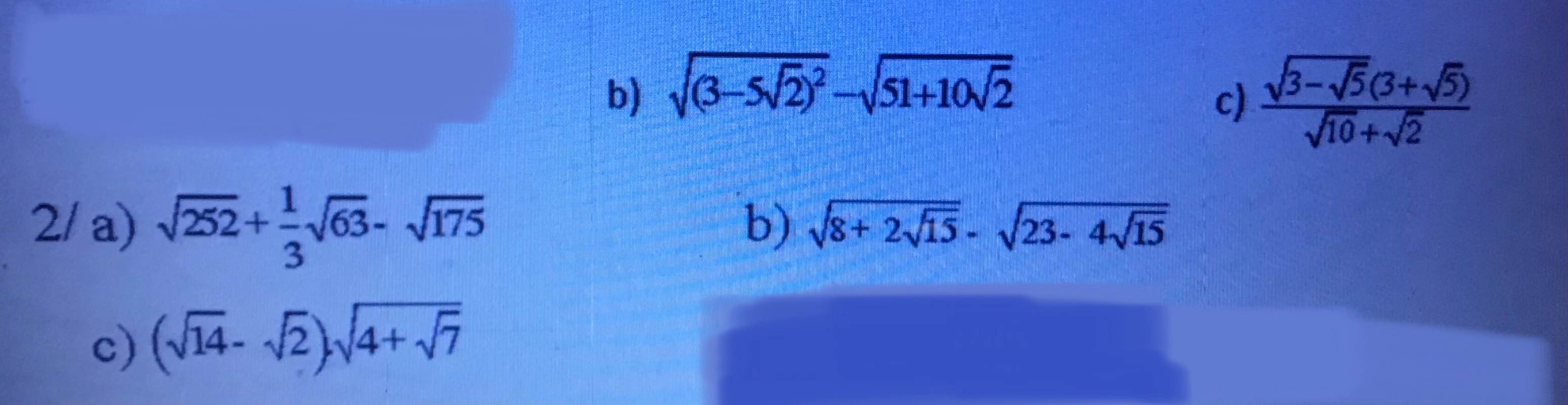


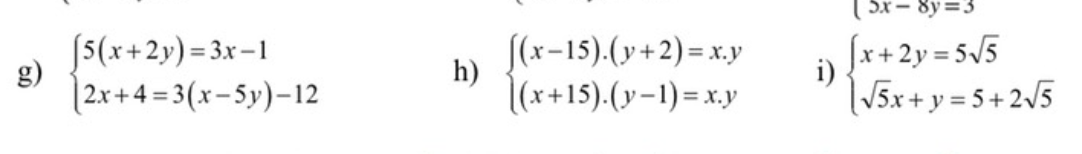




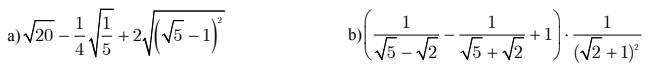

 giải giúp mình ạ mình ko hiểu cách làm lắm
giải giúp mình ạ mình ko hiểu cách làm lắm