2: \(x^2-2x-3m^2=0\)
\(\text{Δ}=\left(-2\right)^2-4\cdot1\left(-3m^2\right)=12m^2+4>0\forall m\)
=>Phương trình luôn có hai nghiệm
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=2\\x_1x_2=\dfrac{c}{a}=-3m^2\end{matrix}\right.\)
\(\left(x_1-x_2\right)^2=\left(x_1+x_2\right)^2-4x_1x_2\)
\(=2^2-4\cdot\left(-3m^2\right)=4+12m^2\)
\(\dfrac{x_1}{x_2}-\dfrac{x_2}{x_1}=\dfrac{8}{3}\)
=>\(\dfrac{x_1^2-x_2^2}{x_1x_2}=\dfrac{8}{3}\)
=>\(\dfrac{\left(x_1-x_2\right)\left(x_1+x_2\right)}{3m^2}=\dfrac{8}{3}\)
=>\(\left(x_1-x_2\right)\cdot2=\dfrac{8}{3}\cdot3m^2=8m^2\)
=>\(x_1-x_2=4m^2\)
=>\(\left(x_1-x_2\right)^2=16m^4\)
=>\(16m^4=12m^2+4\)
=>\(4m^4=3m^2+1\)
=>\(4m^4-3m^2-1=0\)
=>\(4m^4-4m^2+m^2-1=0\)
=>\(\left(m^2-1\right)\left(4m^2+1\right)=0\)
=>\(m^2-1=0\)
=>\(m=\pm1\)
\(\Delta'=1+3m^2>0;\forall m\) nên pt luôn có 2 nghiệm pb
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=-3m^2\ne0\Rightarrow m\ne0\end{matrix}\right.\)
\(\dfrac{x_1^2-x_2^2}{x_1x_2}=\dfrac{8}{3}\)
\(\Rightarrow\left(x_1-x_2\right)\left(x_1+x_2\right)=\dfrac{8}{3}x_1x_2\)
\(\Rightarrow2\left(x_1-x_2\right)=-8m^2\)
\(\Rightarrow x_1-x_2=-4m^2\)
Kết hợp hệ thức Viet: \(\Rightarrow\left\{{}\begin{matrix}x_1-x_2=-4m^2\\x_1+x_2=2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x_1=-2m^2+1\\x_2=2m^2+1\end{matrix}\right.\)
Thế vào \(x_1x_2=-3m^2\)
\(\Leftrightarrow\left(-2m^2+1\right)\left(2m^2+1\right)=-3m^2\)
\(\Leftrightarrow4m^4-3m^2-1=0\)
\(\Rightarrow\left[{}\begin{matrix}m^2=1\\m^2=-\dfrac{1}{4}\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow m=\pm1\)
không cần làm hết đâu ạ chỉ cần 2,3 câu là đc ạ
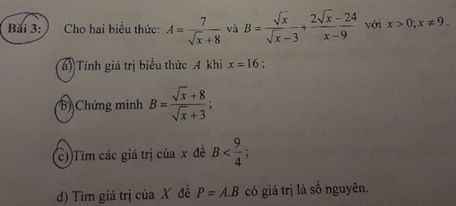
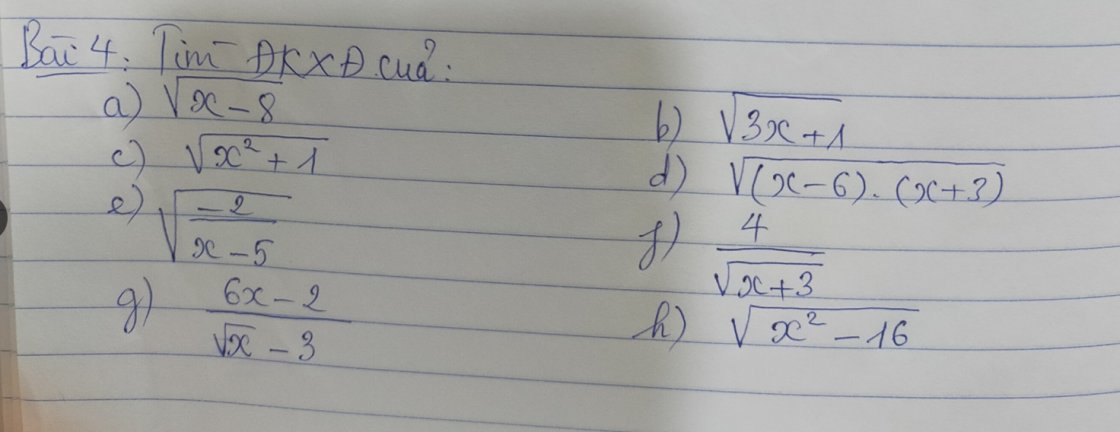
không cần làm câu c đâu ạ, giúp e với nhaaa mn
