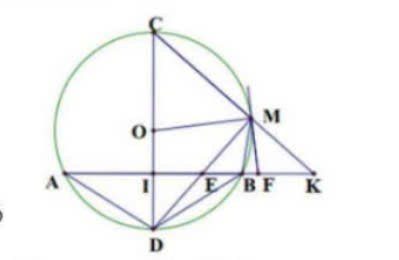
c) Ta có: \(\widehat{DMF}=\widehat{DCM}\); \(\widehat{DCM}=\widehat{MEF}\) (EICM nội tiếp), nên \(\widehat{DMF}=\widehat{EFM}\Rightarrow\Delta MEF\) cân tại F =>FM=EM. Mà △MEK vuông tại F, nên F là trung điểm EK.
d) Dễ thấy MD là phân giác trong của △AMB => MK là phân giác ngoài của △AMB.
Đặt \(a=EA;b=EB\Rightarrow IE=IB-EB=\dfrac{a+b}{2}-b=\dfrac{a-b}{2}\)
Ta có: \(\dfrac{KB}{KA}=\dfrac{EA}{EB}\Rightarrow\dfrac{KB}{AB}=\dfrac{EA}{EA-EB}\Rightarrow KB=\dfrac{EA.AB}{EA-EB}=\dfrac{b.\left(a+b\right)}{\left(a-b\right)}\)
\(\dfrac{BE}{BK}=\dfrac{b}{\dfrac{b\left(a+b\right)}{\left(a-b\right)}}=\dfrac{\left(a-b\right)}{a+b}\)
\(\dfrac{IE}{IA}=\dfrac{\dfrac{a-b}{2}}{\dfrac{a+b}{2}}=\dfrac{a-b}{a+b}\)=>đpcm.
P/s: mình đang buồn ngủ nên giải cách này cho nhanh :D, chứ không biết cách nào hay hơn nữa (thật ra nếu học cao hơn thì có thể dùng hệ thức trong hàng điểm điều hoà để thử, nhưng mình thử không ra :)