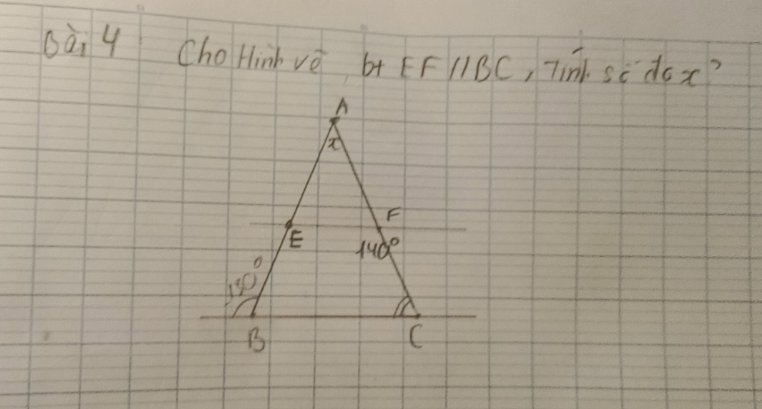
EF//BC
=>\(\widehat{BEF}=130^0\)
Ta có: \(\widehat{BEF}+\widehat{AEF}=180^0\)(hai góc kề bù)
=>\(\widehat{AEF}+130^0=180^0\)
=>\(\widehat{AEF}=50^0\)
Ta có: \(\widehat{AFE}+\widehat{EFC}=180^0\)(hai góc kề bù)
=>\(\widehat{AFE}+140^0=180^0\)
=>\(\widehat{AFE}=40^0\)
Xét ΔAEF có \(\widehat{AEF}+\widehat{AFE}+\widehat{FAE}=180^0\)
=>\(x+50^0+40^0=180^0\)
=>\(x=90^0\)

 hính đúng k sai
hính đúng k sai



 Làm đúng đề nhé. Đề k sai
Làm đúng đề nhé. Đề k sai






