Có 4 góc kề nhau và bằng nhau được tạo thành, xếp thành góc bẹt, mỗi góc tạo bởi 2 thanh chắn vòm cửa.
Do đó, mỗi góc có số đo: \(180^\circ : 4 = 45^\circ \)
Có 4 góc kề nhau và bằng nhau được tạo thành, xếp thành góc bẹt, mỗi góc tạo bởi 2 thanh chắn vòm cửa.
Do đó, mỗi góc có số đo: \(180^\circ : 4 = 45^\circ \)
Trên mặt đồng hồ ở Hình 1, quan sát hai góc: góc tạo bởi kim giờ và kim phút; góc tạo bởi kim phút và kim giây.

Hai góc đó có liên hệ gì đặc biệt?
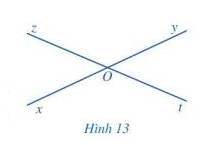
Quan sát hai góc xOz và yOt ở Hình 13, trong đó, Ox và Oy là hai tia đối nhau, Oz và Ot cũng là hai tia đối nhau và cho biết:
a) Cạnh Ox của góc xOz là tia đối của cạnh nào của góc yOt.
b) Cạnh Oz của góc xOz là tia đối của cạnh nào của góc yOt.
a) Tìm hai góc kề nhau trong mỗi hình 18a, 18b:
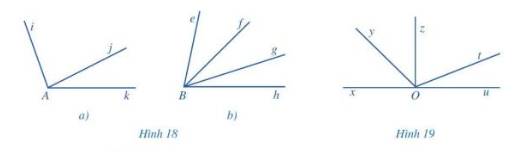
b) Tìm hai góc kề bù ở Hình 19.
c) Tìm hai góc đối đỉnh trong mỗi hình 20a, 20b, 20c, 20d:

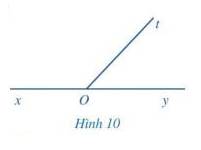
Quan sát hai góc xOt và yOt ở Hình 10, trong đó Ox và Oy là hai tia đối nhau.
a) Hai góc xOt và yOt có kề nhau không?
b) Tính \(\widehat {xOt} + \widehat {yOt}\)
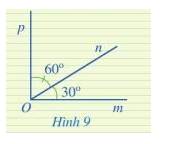
Ở Hình 9, hai góc mOn và pOn có là hai góc kề nhau hay không? Tính số đo của góc mOp.
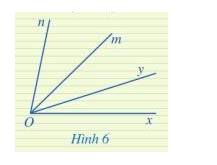
Ở Hình 6, hai góc xOy và mOn có phải là hai góc kề nhau hay không? Vì sao?
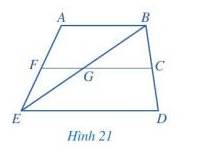
Quan sát Hình 21 và chỉ ra:
a) Hai góc kề nhau;
b) Hai góc kề bù (khác góc bẹt) ;
c) Hai góc đối đỉnh( khác góc bẹt và góc không).
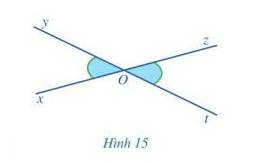
Quan sát Hình 15 và giải thích vì sao:
a) Hai góc xOy và yOz là hai góc kề bù;
b) Hai góc yOz và zOt là hai góc kề bù;
c) \(\widehat {xOy} + \widehat {yOz} = \widehat {yOz} + \widehat {zOt}\) và \(\widehat {xOy} = \widehat {zOt}\)
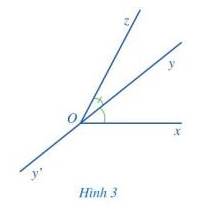
Quan sát hai góc xOy và zOy ở Hình 3.
a) Nêu đỉnh chung và cạnh chung của hai góc xOy và zOy.
b) Vẽ tia đối Oy’ của tia Oy.
c) Hai tia Ox và Oz có nằm về hai phía của đường thẳng yy’ hay không?