Câu 3:
Theo Vi-et, ta có;
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=3\\x_1x_2=\dfrac{c}{a}=-5\end{matrix}\right.\)
\(x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2=3^2-2\cdot\left(-5\right)=19\)
\(T=G\left(x_1\right)\cdot G\left(x_2\right)\)
\(=\left(x_1^2-4\right)\left(x_2^2-4\right)\)
\(=\left(x_1x_2\right)^2-4\left(x_1^2+x_2^2\right)+16\)
\(=\left(-5\right)^2-4\cdot19+16\)
=25+16-76
=25-60
=-35
Câu 4: ĐKXĐ: \(\left\{{}\begin{matrix}3x-5>=0\\7-3x>=0\end{matrix}\right.\)
=>\(\dfrac{5}{3}< =x< =\dfrac{7}{3}\)
\(\sqrt{3x-5}+\sqrt{7-3x}=9x^2-36x+38\)
=>\(\sqrt{3x-5}-1-1-\sqrt{7-3x}=9x^2-18x-18x+36\)
=>\(\dfrac{3x-5-1}{\sqrt{3x-5}+1}-\left(1+\sqrt{7-3x}\right)=\left(x-2\right)\left(9x-18\right)\)
=>\(\dfrac{3x-6}{\sqrt{3x-5}+1}-\dfrac{7-3x-1}{\sqrt{7-3x}-1}=\left(x-2\right)\left(9x-18\right)\)
=>\(\dfrac{3\left(x-2\right)}{\sqrt{3x-5}+1}+\dfrac{3\left(x-2\right)}{\sqrt{7-3x}-1}-\left(x-2\right)\left(9x-18\right)=0\)
=>\(\left(x-2\right)\left(\dfrac{3}{\sqrt{3x-5}+1}+\dfrac{3}{\sqrt{7-3x}-1}-9x+18\right)=0\)
=>x-2=0
=>x=2(nhận)
Câu 1 :
\(4\sqrt{x+3}=1+4x-\dfrac{1}{x}\left(x\ge-3;x\ne0\right)\)
\(\Leftrightarrow4x\sqrt{x+3}=x+4x^2-1\)
\(\Leftrightarrow4x^2-4x\sqrt{x+3}+x+3-4=0\)
\(\Leftrightarrow\left(2x-\sqrt{x+3}\right)^2=4\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-\sqrt{x+3}=2\\2x-\sqrt{x+3}=-2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x+3}=2x-2\left(1\right)\\\sqrt{x+3}=2x+2\left(2\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow\left\{{}\begin{matrix}2x-2\ge0\\x+3=4x^2-8x+4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge1\\4x^2-9x+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge1\\\left[{}\begin{matrix}x=\dfrac{9+\sqrt{65}}{8}\\x=\dfrac{9-\sqrt{65}}{8}\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow x=\dfrac{9+\sqrt{65}}{8}\)
\(\left(2\right)\Leftrightarrow\left\{{}\begin{matrix}2x+2\ge0\\x+3=4x^2+8x+4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-1\\4x^2+7x+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-1\\\left[{}\begin{matrix}x=\dfrac{-7+\sqrt{33}}{8}\\x=\dfrac{-7-\sqrt{33}}{8}\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow x=\dfrac{-7+\sqrt{33}}{8}\)
Vậy \(x\in\left\{x=\dfrac{-7+\sqrt{33}}{8};x=\dfrac{9+\sqrt{65}}{8}\right\}\)
Câu 6 :
\(x^2-y^2+2\left(3x+y\right)=29\)
\(\Leftrightarrow x^2-6x+9-\left(y^2-2y+1\right)=28\)
\(\Leftrightarrow\left(x-3\right)^2-\left(y-1\right)^2=28\)
\(\Leftrightarrow\left(x-3+y-1\right)\left(x-3-y+1\right)=28\)
\(\Leftrightarrow\left(x+y-4\right)\left(x-y-2\right)=28\)
\(\Leftrightarrow\left(x+y-4\right);\left(x-y-2\right)\in U\left(28\right)=\left\{-1;1;-2;2;-4;4;-7;7;-14;14;-28;28\right\}\)
\(\Leftrightarrow\left(x;y\right)=\left(-5;7\right);\left(-2;1\right);\left(-7;-3\right)\) \(\left(x;y\in Z\right)\)
Vậy \(\left(x;y\right)=\left(-5;7\right);\left(-2;1\right);\left(-7;-3\right)\)









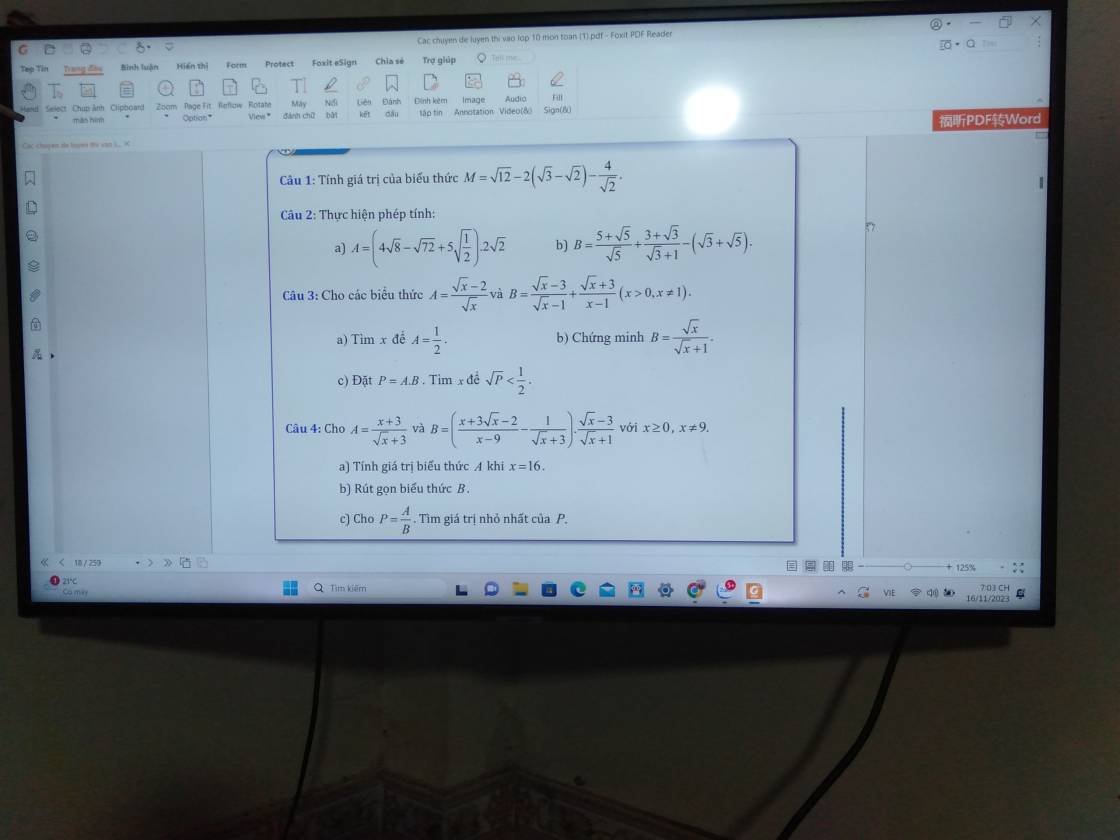



 Giúp tớ câu 4 hoặc câu 5 với ạ
Giúp tớ câu 4 hoặc câu 5 với ạ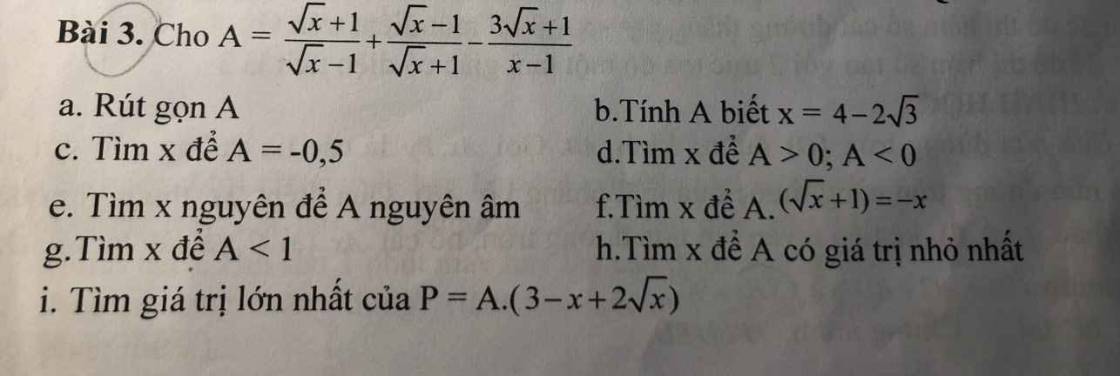 cíu cíu
cíu cíu cíu tui cíu tui
cíu tui cíu tui cíu tui cíu tui
cíu tui cíu tui
 cíu lẹ cíu lẹ
cíu lẹ cíu lẹ 
 cíu tui cíu tui
cíu tui cíu tui