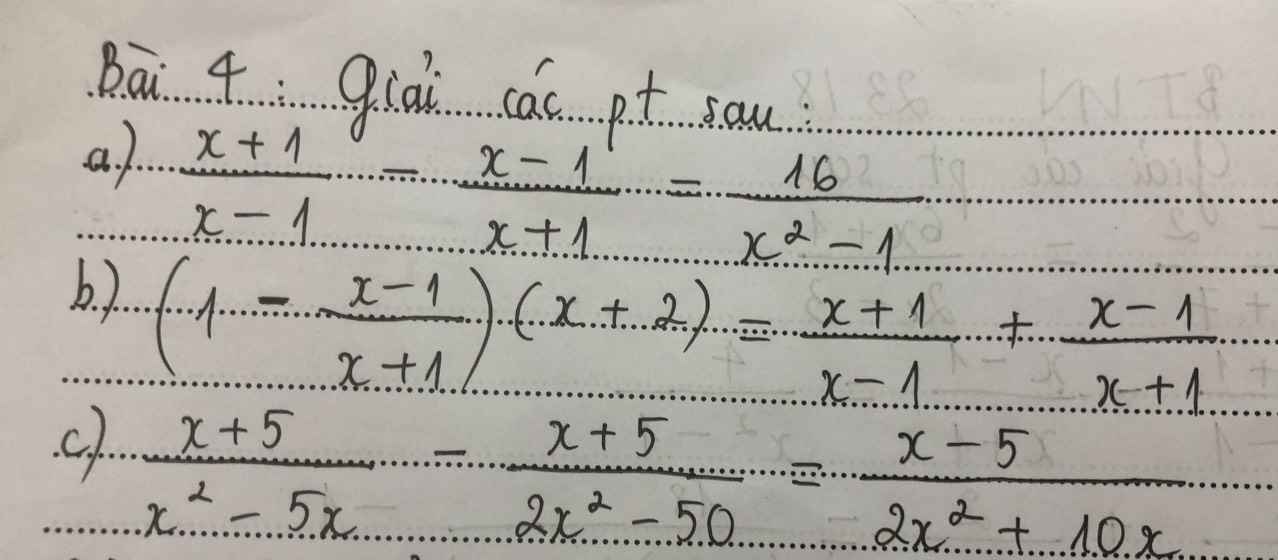b) \(...\left(\dfrac{x+1-x+1}{x+1}\right)\left(x+2\right)=\dfrac{\left(x+1\right)^2+\left(x-1\right)^2}{\left(x-1\right)\left(x+1\right)}\left(x\ne\pm1\right)\)
\(\Leftrightarrow\dfrac{2\left(x+2\right)}{x+1}=\dfrac{\left(x+1+x-1\right)^2-2\left(x-1\right)\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}\)
\(\Leftrightarrow\dfrac{2\left(x+2\right)\left(x-1\right)}{\left(x+1\right)\left(x-1\right)}=\dfrac{4x^2-2\left(x^2-1\right)}{\left(x+1\right)\left(x-1\right)}\)
\(\Leftrightarrow2\left(x^2+x-2\right)=4x^2-2x^2+2\)
\(\Leftrightarrow2x^2+2x-4=4x^2-2x^2+2\)
\(\Leftrightarrow2x=6\Leftrightarrow x=3\left(tm\right)\)
Vậy... \(x=3\)
`c)(x+5)/(x^2-5x)-(x+5)/(2x^2-50)=(x-5)/(2x^2+10x)` `(ĐK:x<>+-5;x<>0)`
`<=>(x+5)/(x(x-5))-(x+5)/(2(x^2-25))=(x-5)/(2x(x+5))`
`<=>(2(x+5)^2)/(2x(x-5)(x+5))-(x(x+5))/(2x(x+5)(x-5))=(x-5)^2/((2x(x+5)(x-5))`
`<=>2(x+5)^2-x(x+5)=(x-5)^2`
`<=>2(x^2+10x+25)-x^2-5x=x^2-10x+25`
`<=>2x^2+20x+50-x^2-5x=x^2-10x+25`
`<=>x^2+15x+50=x^2-10x+25`
`<=>15x+50=-10x+25`
`<=>15x+10x=25-50`
`<=>25x=-25`
`<=>x=-1(tm)`