Chọn A.
Ta có: 
Hàm số y =
-
x
3
-
3
x
2
+
9
x
+
20
đồng biến khi và chỉ khi 
Cho hàm số: y = x - 2 x + 3
Khẳng định nào sau đây là đúng?
A. Hàm số đồng biến trên từng khoảng xác định;
B. Hàm số đồng biến trên khoảng (- ∞ ;+ ∞ );
C. Hàm số nghịch biến trên từng khoảng xác định;
D. Hàm số nghịch biến trên khoảng (- ∞ ;+ ∞ ).
Hàm số y = \(\sqrt{2x-x^{^2}}\) nghịch biến trên khoảng nào sau?
A. (0;1)
B. (0;2)
C. (1;2)
D. (1;+∞)
Câu 48: Cho hàm số y=f(x) có đạo hàm liên tục trên R và \(f'\left(x\right)=x\left(2x-1\right)\left(x^2+3\right)+2\). Hàm số \(y=f\left(3-x\right)+2x+2023\) đồng biến trên khoảng nào trong các khoảng sau?
A: \(\left(-\infty;3\right)\)
B: (3;5)
C: (2;5/2)
D: (5/2;3)
Câu 50: Cho hàm số y=f(x) có đạo hàm \(f'\left(x\right)=\left(x-1\right)^2\cdot\left(x^2-2x\right)\) với \(\forall x\in R\). Có bao nhiêu giá trị nguyên dương của tham số m để hàm số \(f\left(x^2-8x+m\right)\) có 5 điểm cực trị?
trong các hàm số sau hàm số nào đồng biến trên R: A. y= 2x-1/x+2 B. y= -x^3+x^2-5x C. y= x^3+2x+1 D.-x^4-2x^2+3
Cho hàm số y = f ( x ) liên tục trên R và có đạo hàm f ' ( x ) = ( 1 - x ) 2 ( x + 1 ) 3 ( 3 - x ) . Hàm số y = f ( x ) đồng biến trên khoảng nào dưới đây
Cho hàm số y = x − 2 x − 1 . Xét các mệnh đề sau:
1. Hàm số đã cho đồng biến trên − ∞ ; 1 ∪ 1 ; + ∞ .
2. Hàm số đã cho đồng biến trên ℝ \ 1 .
3. Hàm số đã cho đồng biến trên từng khoảng xác định.
4. Hàm số đã cho đồng biến trên các khoảng − ∞ ; − 1 và − 1 ; + ∞ .
Số mệnh đề đúng là
A. 3
B. 2
C. 1
D. 4
Hàm số y=f(x) có đồ thị y=f '(x) như hình vẽ
.
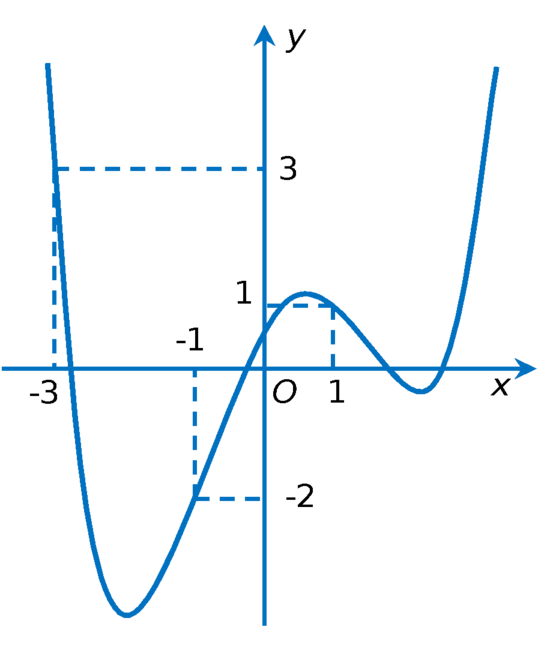
Xét hàm số g ( x ) = f ( x ) - 1 3 x 3 - 3 4 x 2 + 3 2 x + 2017
Trong các mệnh đề dưới đây
(I) .g(0)<g(1)
(II) . m i n x ∈ [ - 3 ; 1 ] g ( x ) = g ( - 1 )
(III) Hàm số g(x)nghịch biến trên (-3;-1).
(IV). m a x x ∈ [ - 3 ; 1 ] g ( x ) = m a x { g ( - 3 ) , g ( 1 ) }
Số mệnh đề đúng là
A.2.
B.1.
C.3
D.4.
Bài 1 : Định m để hàm số
1. Y=2x^3-3(2m+1)x^2 + 6m(m+1) Đồng biến trên khoảng (2; dương vô cùng)
2. Y= x^3+ (m-1)x^2 -(2m^2 +3m+2)x Nghịch biến trên (2; dvc)
Cho hàm số y=f(x) liên tục trên nửa khoảng [-1;2) có bảng biến thiên như hình vẽ. Khẳng định nào sau đây là đúng?
|
|
|
||
|
|
+ |
||
|
|
3 |
||
A.Không tồn tại giá trị nhỏ nhất của hàm số 
B.Hàm số nghịch biến trên khoảng 
C. 
D. Đường thẳng 
là tiệm cận đứng của đồ thị hàm số 
Hàm số y = - x 4 2 + 1 đồng biến trên khoảng:
A. (- ∞ ; 0); B. (1; + ∞ );
C. (-3; 4); D. (- ∞ ; 1).
