Đáp án D
Hàm số có tập xác định là ℝ ⇔ 4 x − 2 x + m > 0 , ∀ x ∈ ℝ ⇔ m > 2 x − 4 x ∀ x ∈ ℝ
Đặt t = 2 x > 0 ⇒ m > t − t 2 ∀ t > 0 ⇔ m > max t > 0 f t ⇔ m > 1 4
Đáp án D
Hàm số có tập xác định là ℝ ⇔ 4 x − 2 x + m > 0 , ∀ x ∈ ℝ ⇔ m > 2 x − 4 x ∀ x ∈ ℝ
Đặt t = 2 x > 0 ⇒ m > t − t 2 ∀ t > 0 ⇔ m > max t > 0 f t ⇔ m > 1 4
Cho các phát biểu sau
(1) Đơn giản biểu thức M = a 1 4 - b 1 4 a 1 4 + b 1 4 a 1 2 + b 1 2 ta được M = a - b
(2) Tập xác định D của hàm số y = log 2 ln 2 x - 1 là D = e ; + ∞
(3) Đạo hàm của hàm số y = log 2 ln x là y ' = 1 x ln x . ln 2
(4) Hàm số y = 10 log a x - 1 có đạo hàm tại mọi điểm thuộc tập xác định
Số các phát biểu đúng là
A. 6
B. 1
C. 3
D. 4
Hàm số y = ln x 2 − 2 m x + 4 có tập xác định D = ℝ khi các giá trị của tham số m là
A. m < 2
B. m < − 2 m > 2
C. m = 2
D. − 2 < m < 2
Một học sinh giải bài toán “Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = m x 3 + m x 2 + m − 2 x + 10 đồng biến trên i” theo các bước như sau:
Bước 1: Hàm số xác định trên i, và y ' = 3 m x 2 + 2 m x + m − 2
Bước 2: Yêu cầu bài toán tương đương với y ' > 0, ∀ x ∈ ℝ ⇔ 3 m x 2 + 2 m x + m − 2 > 0, ∀ x ∈ ℝ
Bước 3: ⇔ a = 3 m > 0 Δ ' = 6 m − 2 m 2 < 0 ⇔ m < 0 m > 3 m > 0
Bước 4: ⇔ m > 3. Vậy m>3
Hỏi học sinh này đã bắt đầu sai ở bước nào?
A. Bước 2
B. Bước 3
C. Bước 1
D. Bước 4
Cho hàm số y = f x xác định, liên tục và có đạo hàm trên đoạn a , b . Xét các khẳng định sau:
1. Hàm số f x đồng biến trên a ; b thì f ' x > 0 , ∀ x ∈ a ; b
2. Giả sử f a > f c > f b , ∀ x ∈ a ; b suy ra hàm số nghịch biến trên a ; b
3. Giả sử phương trình f ' x = 0 có nghiệm là x = m khi đó nếu hàm số y = f x đồng biến trên m ; b thì hàm số y = f x nghịch biến trên a , m
4. Nếu f ' x ≥ 0 , ∀ x ∈ a ; b , thì hàm số đồng biến trên a ; b
Số khẳng định đúng trong các khẳng định trên là
A. 1
B. 0
C. 3
D. 2
Cho hàm số y=f(x) xác định trên tập D = ℝ \ { 1 } và liên tục trên mỗi khoảng xác định và có bảng biến thiên sau:
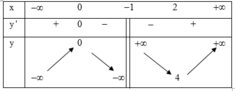
Tìm tập hợp tất cả các giá trị của tham số m sao cho phương trình f(x)=m-1 có hai nghiệm thực phân biệt là:
A. m < 1 m > 5
B. 1<m<5
C. m<1
D. m>5
Cho các mệnh đề sau đây:
(1) Hàm số f ( x ) = log 2 2 x - log 2 x 4 + 4 có tập xác định D = [ 0 ; + ∞ )
(2) Hàm số y = log a x có tiệm cận ngang
(3) Hàm số y = log a x ; 0 < a < 1 và Hàm số y = log a x , a > 1 đều đơn điệu trên tập xác định của nó
(4) Bất phương trình: log 1 2 5 - 2 x 2 - 1 ≤ 0 có 1 nghiệm nguyên thỏa mãn.
(5) Đạo hàm của hàm số y = ln 1 - cos x là sin x 1 - cos x 2
Hỏi có bao nhiêu mệnh đề đúng:
A. 0
B. 2
C. 3
D.1
Tìm tất cả các giá trị thực của tham số m để bất phương trình ( m + 1 ) x 2 - 2 ( m + 1 ) x + 4 ≥ 0 ( 1 ) có tập nghiệm S = ℝ ?
A. m > - 1
B. - 1 ≤ m ≤ 3
C. - 1 < m ≤ 3
D. - 1 < m < 3
Cho f x là hàm đa thức thỏa mãn f x - x f 1 - x = x 4 - 5 x 3 + 12 x 2 - 4 ∀ x ∈ ℝ . Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = f x trên tập D = x ∈ ℝ | x 4 - 10 x 2 + 9 ≤ 0 . Giá trị của 21 m + 6 M + 2019 bằng
A. 2235.
B. 2319.
C. 3045.
D. 3069.
Cho hàm số y=f(x) có đạo hàm xác định trên tập ℝ / 0 và đồ thị hàm số y=f(x) như hình vẽ bên dưới. Có bao nhiêu giá trị nguyên của tham số m để phương trình f cos 2 x = m có nghiệm?
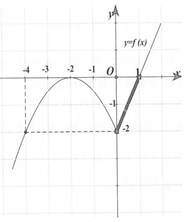
A. Không tồn tại m
B. 1
C. 2
D. 3