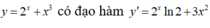Các câu hỏi tương tự
Hàm số nào sau đây có đạo hàm là
y
1
(
x
-
3
)
ln
4
A.
y
log
4
(
x
-
3
)
B.
y
...
Đọc tiếp
Hàm số nào sau đây có đạo hàm là y ' = 1 ( x - 3 ) ln 4
A. y = log 4 ( x - 3 )
B. y = 4 x - 3
C. y = 1 ln 4 ( x - 3 )
D. Đáp án khác
Hàm số
y
f
(
x
)
có đạo hàm
f
(
x
)
(
x
-
1
)
2
(
x
-
3
)
với mọi x. Phát biểu nào sau đây đúng? A. Hàm số có 1 điểm cực đại B. Hàm số không có cực trị C. Hàm số có 2 điểm cực trị D. Hàm số có đúng 1 điểm cực trị
Đọc tiếp
Hàm số y = f ( x ) có đạo hàm f ' ( x ) = ( x - 1 ) 2 ( x - 3 ) với mọi x. Phát biểu nào sau đây đúng?
A. Hàm số có 1 điểm cực đại
B. Hàm số không có cực trị
C. Hàm số có 2 điểm cực trị
D. Hàm số có đúng 1 điểm cực trị
Cho hàm số yf(x)có đạo hàm y
x
2
(
x
-
2
)
. Mệnh đề nào sau đây đúng? A. Hàm số nghịch biến trên R. B. Hàm số đồng biến trên . C. Hàm số nghịch biến trên và D. Hàm số đồng biến trên
Đọc tiếp
Cho hàm số y=f(x)có đạo hàm y'= x 2 ( x - 2 ) . Mệnh đề nào sau đây đúng?
A. Hàm số nghịch biến trên R.
B. Hàm số đồng biến trên ![]() .
.
C. Hàm số nghịch biến trên ![]() và
và ![]()
D. Hàm số đồng biến trên ![]()
Cho hàm số y f(x) có đạo hàm y
x
2
(
x
-
2
)
. Mệnh đề nào sau đây đúng? A. Hàm số nghịch biến trên R. B. Hàm số đồng biến trên (0;2). C. Hàm số nghịch biến trên D. Hàm số đồng biến trên (2;
+
∞
)
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm y'= x 2 ( x - 2 ) . Mệnh đề nào sau đây đúng?
A. Hàm số nghịch biến trên R.
B. Hàm số đồng biến trên (0;2).
C. Hàm số nghịch biến trên ![]()
D. Hàm số đồng biến trên (2; + ∞ )
Cho hàm số yf(x) có đạo hàm và liên tục trên R. Biết rằng đồ thị hàm số yf (x) như hình dưới đây Lập hàm số g(x)f(x)-x^2-x. Mệnh đề nào sau đây đúng? A. B. C. D.
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm và liên tục trên R. Biết rằng đồ thị hàm số y=f '(x) như hình dưới đây
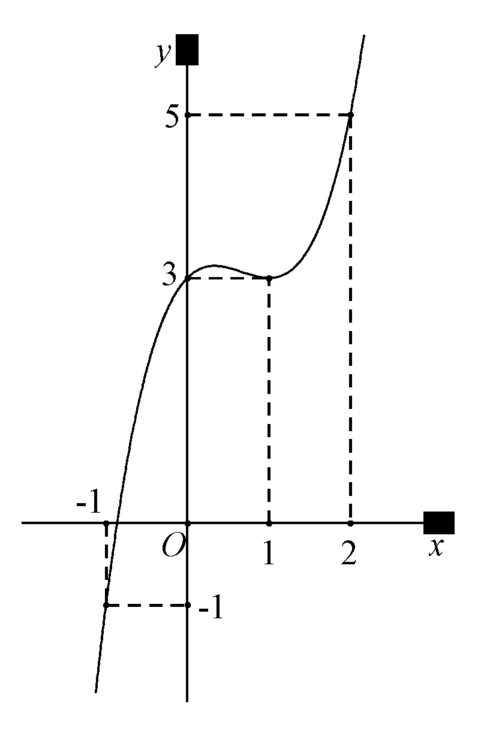
Lập hàm số g(x)=f(x)-x^2-x. Mệnh đề nào sau đây đúng?
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Cho hàm số f(x) có đạo hàm
f
(
x
)
x
(
x
-
1
)
(
x
+
2
)
2
Kết luận nào sau đây là đúng? A. Hàm số f(x) nghịch biến trên khoảng (-∞;1). B. Hàm số f(x) đồng biến trên các khoảng (-∞...
Đọc tiếp
Cho hàm số f(x) có đạo hàm f ' ( x ) = x ( x - 1 ) ( x + 2 ) 2
Kết luận nào sau đây là đúng?
A. Hàm số f(x) nghịch biến trên khoảng (-∞;1).
B. Hàm số f(x) đồng biến trên các khoảng (-∞;0) và (1;+∞).
C. Hàm số f(x) đồng biến trên các khoảng và (1;+∞).
D. Hàm số f(x) đồng biến trên các khoảng (1;+∞).
Cho hàm số y f(x) có đạo hàm trên R và có đồ thị của hàm số y f(x) như hình vẽ. Xét hàm số g(x) f
x
2
-
2
Mệnh đề nào sau đây sai? A. Hàm số g(x) nghịch biến trên (0;2) B. Hàm số g(x) đồng biến trên (2;+
∞
) C. Hàm số g(x) nghịch biến trên (-
∞
;-2) D. Hàm số g(x) nghịch biến trên (-1;0).
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm trên R và có đồ thị của hàm số y = f'(x) như hình vẽ. Xét hàm số g(x) = f x 2 - 2
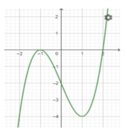
Mệnh đề nào sau đây sai?
A. Hàm số g(x) nghịch biến trên (0;2)
B. Hàm số g(x) đồng biến trên (2;+ ∞ )
C. Hàm số g(x) nghịch biến trên (- ∞ ;-2)
D. Hàm số g(x) nghịch biến trên (-1;0).
Cho hàm số y f(x) có đạo hàm trên R và có đồ thị y f(x) như hình vẽ. Xét hàm số g(x) f(
x
2
-2). Mệnh đề nào sau đây sai? A. Hàm số g(x) nghịch biến trên (0;2). B. Hàm số g(x) đồng biến trên (2;+
∞
). C. Hàm số g(x) nghịch biến trên (-
∞
;-2). D. Hàm số g(x) nghịch biến trên (-1;0).
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm trên R và có đồ thị y = f'(x) như hình vẽ.
Xét hàm số g(x) = f( x 2 -2).
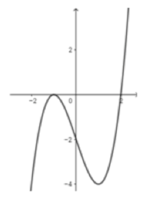
Mệnh đề nào sau đây sai?
A. Hàm số g(x) nghịch biến trên (0;2).
B. Hàm số g(x) đồng biến trên (2;+ ∞ ).
C. Hàm số g(x) nghịch biến trên (- ∞ ;-2).
D. Hàm số g(x) nghịch biến trên (-1;0).
Cho hàm số
f
(
x
)
có đạo hàm
f
(
x
)
x
(
x
-
2
)
3
, với mọi
x
∈
R
. Hàm số đã cho nghịch biến trên khoảng nào sau đây
Đọc tiếp
Cho hàm số f ( x ) có đạo hàm f ' ( x ) = x ( x - 2 ) 3 , với mọi x ∈ R . Hàm số đã cho nghịch biến trên khoảng nào sau đây
![]()
![]()
![]()
![]()
Cho hàm số
y
f
(
x
)
liên tục trên R và có đạo hàm
f
(
x
)
(
1
-
x
)
2
(
x
+
1
)
3
(
3
-
x
)
. Hàm số
y
f
(
x
)
đồng biến trên khoảng nào dưới đây
Đọc tiếp
Cho hàm số y = f ( x ) liên tục trên R và có đạo hàm f ' ( x ) = ( 1 - x ) 2 ( x + 1 ) 3 ( 3 - x ) . Hàm số y = f ( x ) đồng biến trên khoảng nào dưới đây
![]()
![]()
![]()
![]()