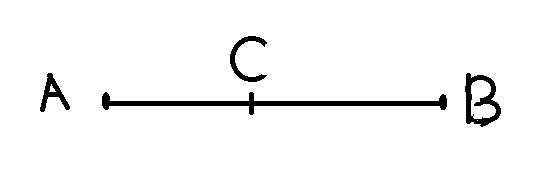
Gọi độ dài cạnh \(AC\) bằng a và độ dài cạnh \(BC=AB-AC=0,09-a\left(m\right)\)
Để điện tích \(q_3\) đặt tại C cân bằng: \(\Leftrightarrow F_{AC}=F_{BC}\)
\(\Leftrightarrow k\cdot\dfrac{\left|q_1\cdot q_3\right|}{r^2_{AC}}=k\cdot\dfrac{\left|q_2\cdot q_3\right|}{r^2_{BC}}\)
\(\Leftrightarrow\dfrac{\left|10^{-7}\cdot q_3\right|}{a^2}=\dfrac{\left|-9\cdot10^{-7}\cdot q_3\right|}{\left(0,09-a\right)^2}\Leftrightarrow\dfrac{1}{a^2}=\dfrac{9}{\left(0,09-a\right)^2}\)
\(\Leftrightarrow8a^2+0,18a-8,1\cdot10^{-3}=0\Leftrightarrow\left[{}\begin{matrix}a=0,0225m=2,25cm\\a=-0,045\left(loại\right)\end{matrix}\right.\)
Vậy đặt \(q_3\) tại điểm C cách A một đoạn 2,25cm.
`q_3` cân bằng `<=>{(\vec{F_[13]} \uparrow \downarrow \vec{F_[23]}),(F_[13]=F_[23]):}`
Vì `q_1;q_2` cùng dấu `=>q_3` nằm giữa đường nối `q_1;q_2`
`=>r_[13]+r_[23]=r_[12]=0,09`
`=>r_[23]=0,09-r_[13]`
Vì `F_[13]=F_[23]=>[|q_1|]/[r_[13]^2]=[|q_2|]/[r_[23]^2]`
`<=>[|-10^[-7]|]/[r_[13]^2]=[|-9.10^[-7]|]/[(0,09-r_[13])^2]`
`<=>r_[13]=0,0225(m)=>r_[23]=0,0675(m)`
Vậy `r_[13]=0,225m ;r_[23]=0,0675 m` thì `q_3` cân bằng








