a) \(\sqrt{a}+\sqrt{b}\le\sqrt{2\left(a+b\right)}\)
\(\Leftrightarrow a+b+2\sqrt{ab}\le2\left(a+b\right)\)
\(\Leftrightarrow a-2\sqrt{ab}+b\ge0\Leftrightarrow\left(\sqrt{a}-\sqrt{b}\right)^2\ge0\left(đúng\right)\)
ĐTXR \(\Leftrightarrow a=b\)
b) Áp dụng BĐT Bunhiacopxki:
\(M^2=\left(1.\sqrt{3x-1}+1.\sqrt{5-3x}\right)^2\le\left(1^2+1^2\right)\left(3x-1+5-3x\right)=2.4=8\)
\(\Rightarrow M^2\le8\Leftrightarrow M\le2\sqrt{2}\)
\(maxM=2\sqrt{2}\Leftrightarrow\) \(\dfrac{1}{\sqrt{3x-1}}=\dfrac{1}{\sqrt{5-3x}}\)\(\Leftrightarrow3x-1=5-3x\Leftrightarrow x=1\left(tm\right)\)
Đúng 0
Bình luận (0)
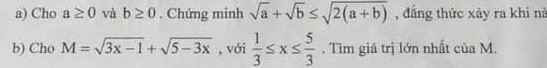
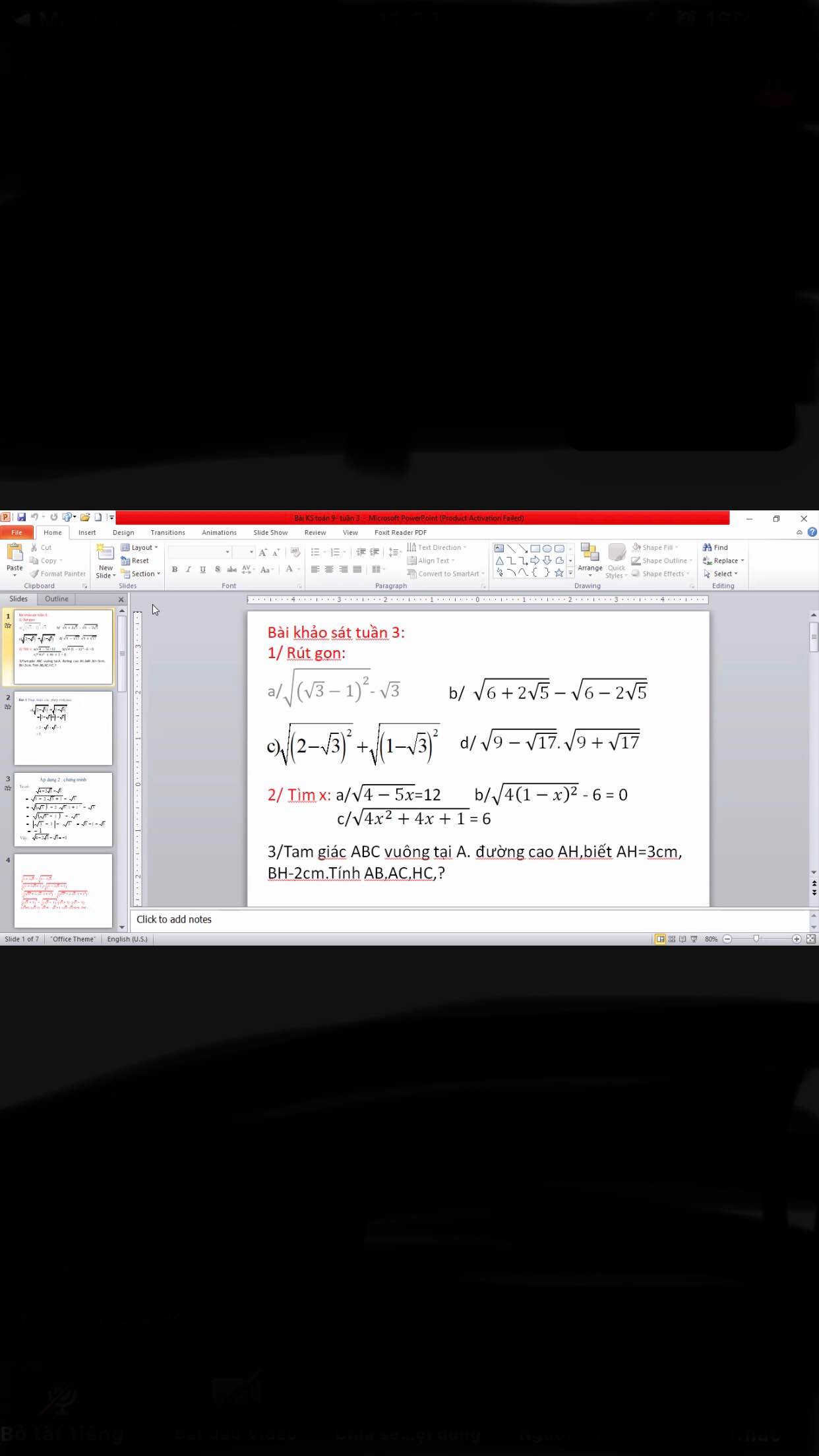
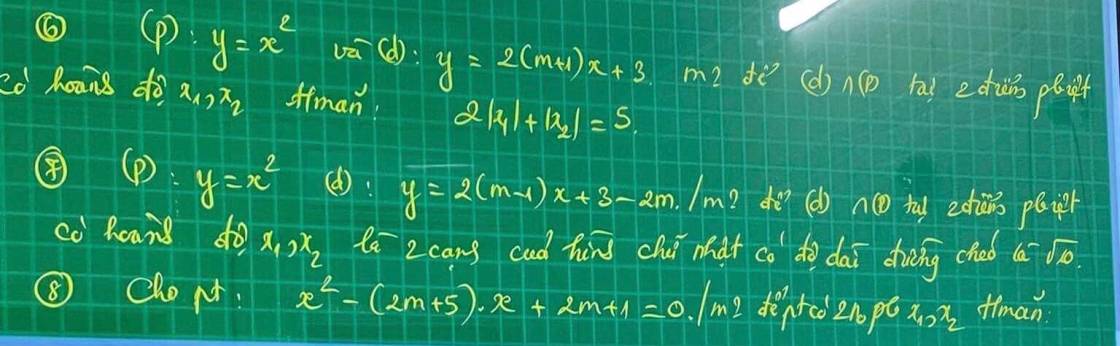
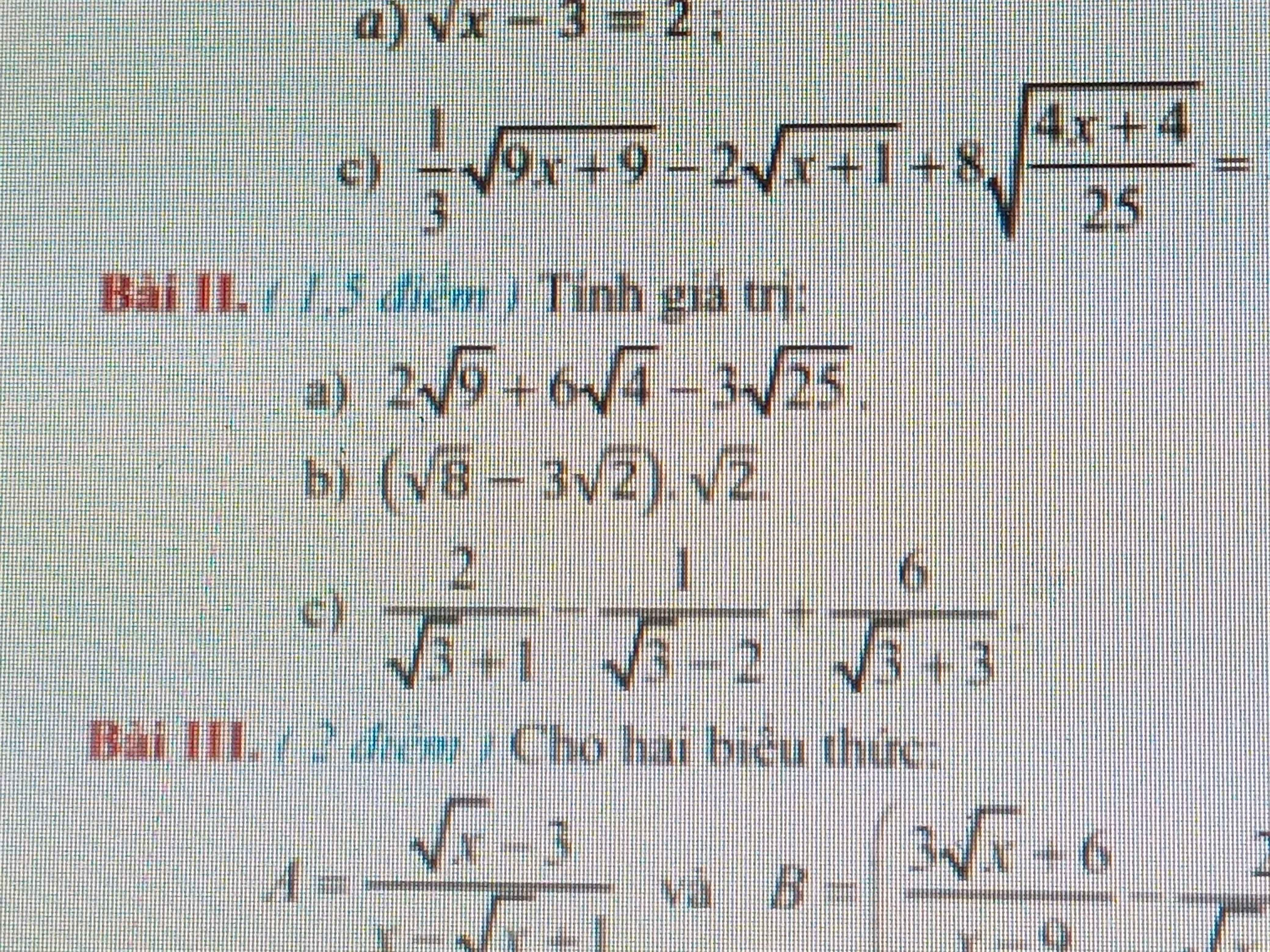
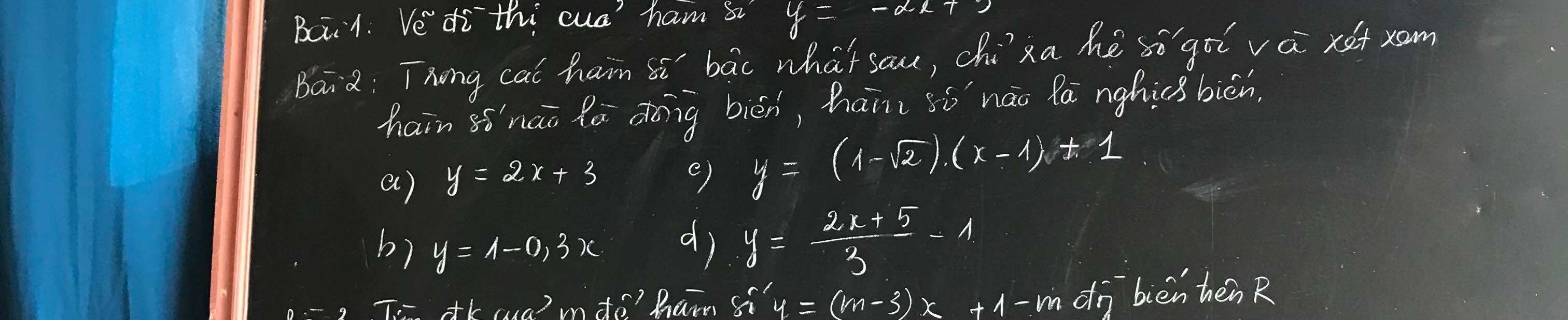
giải hộ mình vs ạ mình cần gấp ạ