
Giúp mình với
Câu 2 Cho hình vuông \(ABCD\). Trên các cạnh \(AD, DC\) lần lượt lấy các điểm \(E, F\) sao cho \(AE = DF\). Chứng minh:
a) Các tam giác \(ADF\) và \(BAE\) bằng nhau;
b) \(BE\) vuông góc với \(AF\).
Câu 3 Cho hình vuông \(ABCD\). Gọi \(I, K\) lần lượt là trung điểm của \(AD\) và \(DC\)
a) Chứng minh rằng \(BI \perp AK\);
b) Gọi \(E\) là giao điểm của \(BI\) và \(AK\). Chứng minh rằng \(CE = AB\).
Câu 2:
a; Xét ΔBAE vuông tại A và ΔADF vuông tại D có
BA=AD
AE=DF
Do đó: ΔBAE=ΔADF
b: ΔBAE=ΔADF
=>\(\hat{AEB}=\hat{DFA}\)
mà \(\hat{DFA}+\hat{DAF}=90^0\) (ΔDAF vuông tại D)
nên \(\hat{AEB}+\hat{DAF}=90^0\)
=>AF⊥BE
Câu 3:
a: Ta có: \(AI=ID=\frac{AD}{2}\)
\(DK=KC=\frac{DC}{2}\)
mà AD=DC
nên AI=ID=DK=KC
Xét ΔADK vuông tại D và ΔBAI vuông tại A có
AD=BA
DK=AI
Do đó: ΔADK=ΔBAI
=>\(\hat{AKD}=\hat{BIA}\)
mà \(\hat{AKD}+\hat{KAD}=90^0\) (ΔADK vuông tại D)
nên \(\hat{KAD}+\hat{BIA}=90^0\)
=>AK⊥BI tại E













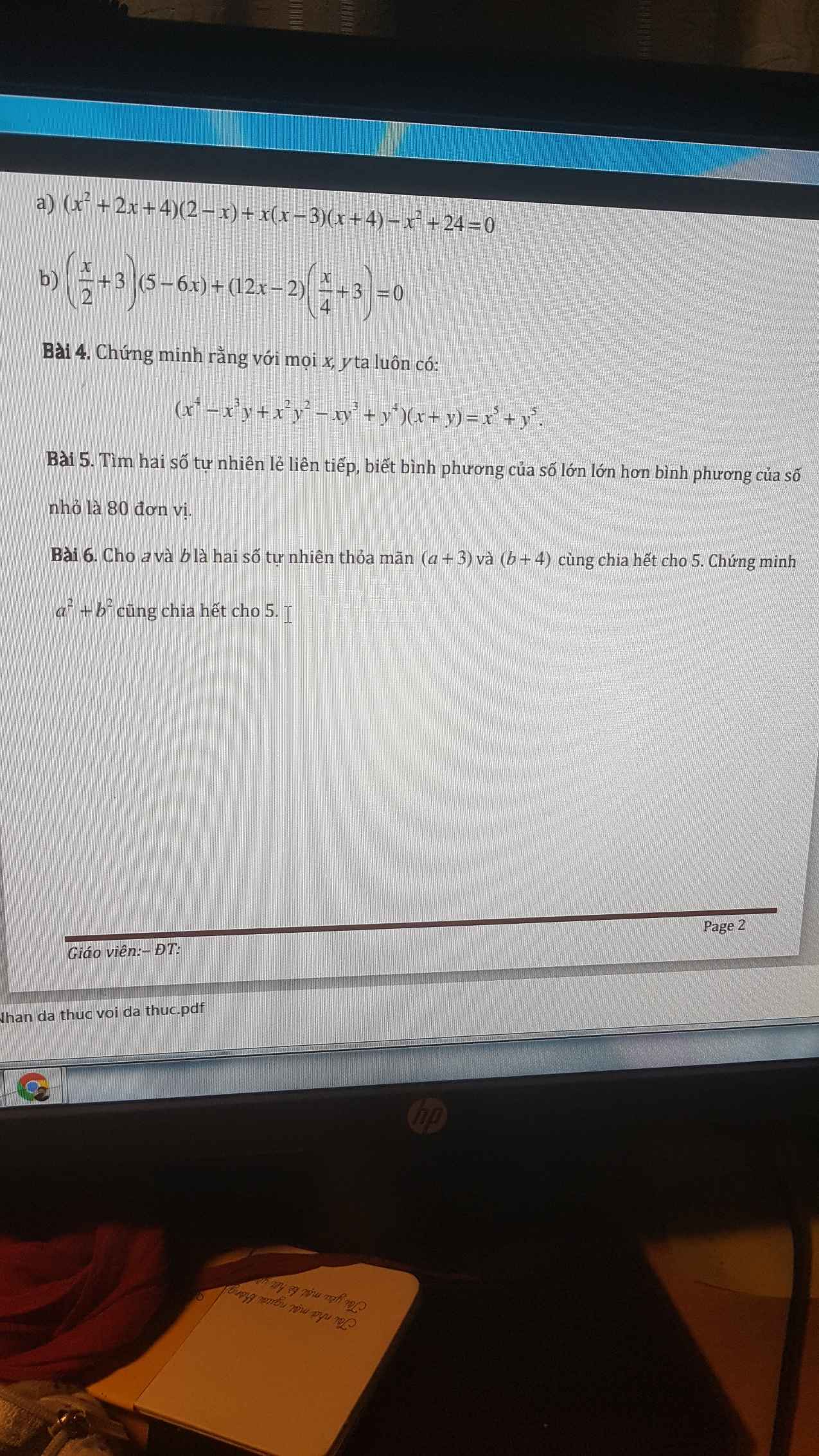

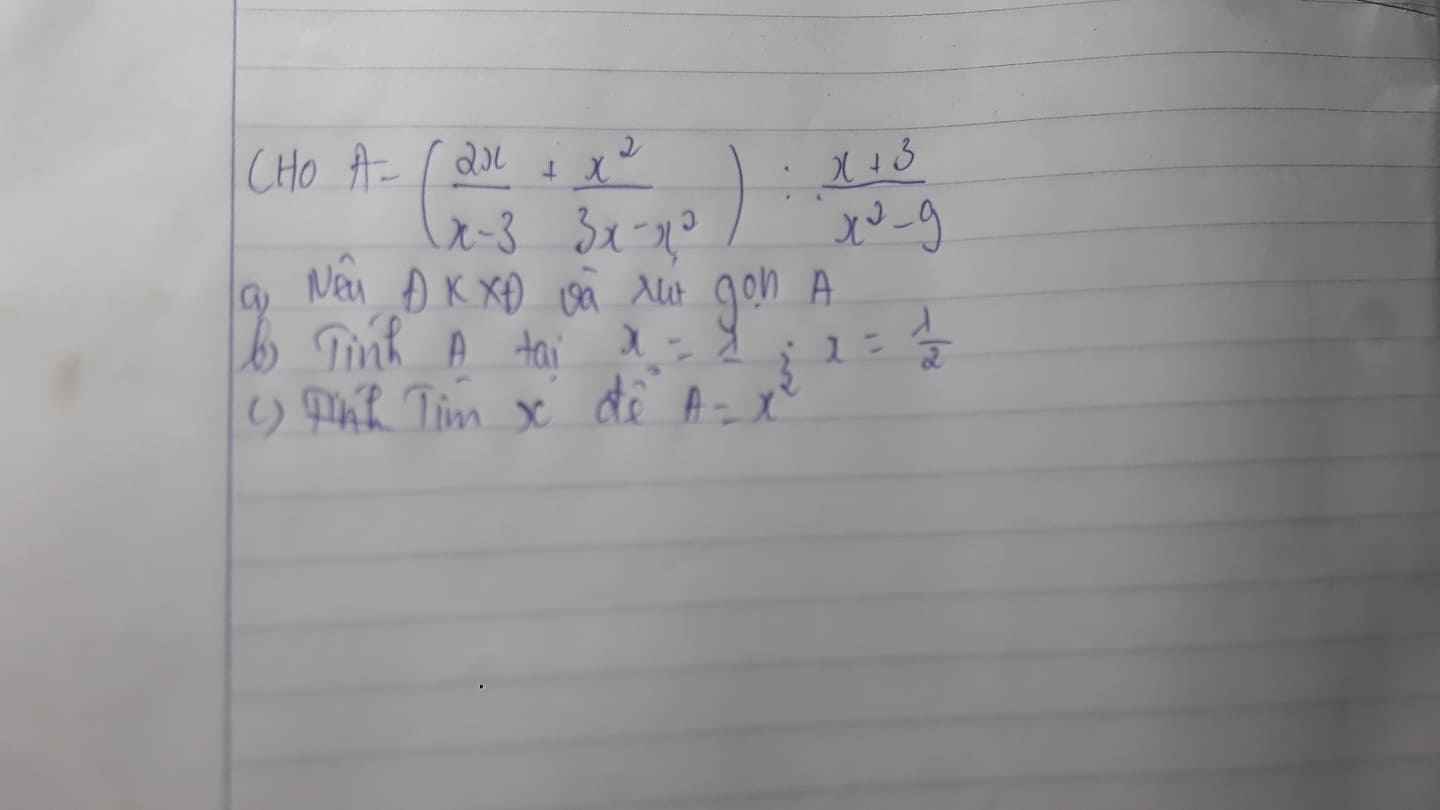



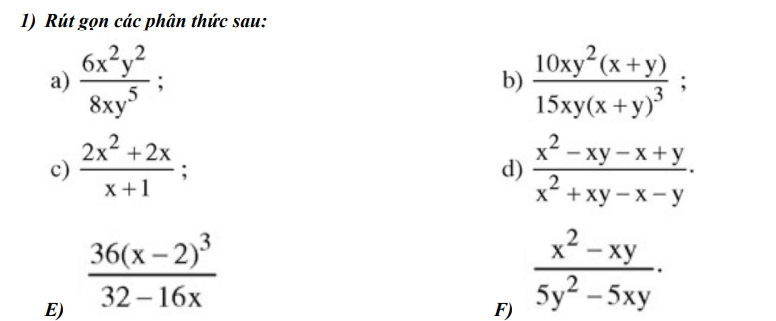

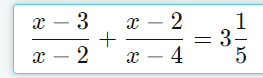 mình cần gấp giúp mình với
mình cần gấp giúp mình với